已知一个袋子里有形状一样仅颜色不同的6个小球，其中白球2个，黑球4个. 现从中随机取球，每次只取一球.
（1）若每次取球后都放回袋中，求事件“连续取球四次，至少取得两次白球”的概率；
（2）若每次取球后都不放回袋中，且规定取完所有白球或取球次数达到五次就终止游戏，记游戏结束时一共取球X次，求随机变量X的分布列与期望
（本题14分）如图，在三棱锥P—ABC中，E、F、G、H分别是AB、AC、PC、BC的中点，且PA=PB，AC=BC．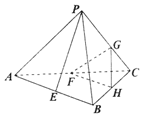
（1）证明：AB⊥PC；（2）证明：PE//平面FGH。
已知命题
：存在
使得
成立，命题
：对于任意
，函数
恒有意义．
（1）若是真命题，求实数
的取值范围；
（2）若
是假命题，求实数的取值范围．
已知点
是圆
上任意一点，过点作
轴的垂线，垂足为
，点
满足
记点的轨迹为曲线
．
（Ⅰ）求曲线的方程；
（Ⅱ）设
，点
在曲线上，且直线
与直线
的斜率之积为
，求
的面积的最大值．
如图，矩形
所在的半平面和直角梯形
所在的半平面成
的二面角，
∥
,
,
,
,
,
．
（Ⅰ）求证：
∥平面
；
（Ⅱ）在线段上求一点
，使锐二面角
的余弦值为
（本题14分）已知椭圆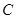
的方程为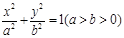
，称圆心在坐标原点
，半径为
的圆为椭圆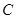的“伴随圆”，椭圆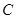的短轴长为2，离心率为
．
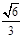（1）求椭圆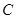及其“伴随圆”的方程；
（2）若直线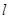
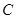与椭圆交于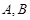
两点，与其“伴随圆”交于
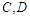两点，当 
时，求△
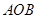面积
的最大值．