已知函数f(x)=f′(1)ex﹣1﹣f(0)x+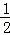 x2,其中e是自然对数的底数,f′(x)为f(x)的导函数.
x2,其中e是自然对数的底数,f′(x)为f(x)的导函数.
(1)求函数f(x)的解析式;
(2)若函数g(x)=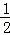 x2+a与函数f(x)的图象在区间[﹣1,2]上恰有两个不同的交点,求实数a的取值范围.
x2+a与函数f(x)的图象在区间[﹣1,2]上恰有两个不同的交点,求实数a的取值范围.
已知 ,直线l:y=-2,动点P到直线l的距离为d,且d=
,直线l:y=-2,动点P到直线l的距离为d,且d= .
.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)直线m:y= 与点P的轨迹交于M、N两点,当
与点P的轨迹交于M、N两点,当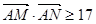 时,求直线m的倾斜角α的取值范围;
时,求直线m的倾斜角α的取值范围;
(Ⅲ)设直线h与点P的轨迹交于C、D两点,写出命题“如果直线h过点B,那么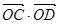 =-12”的逆命题,并判断该逆命题的真假,请说明理由.
=-12”的逆命题,并判断该逆命题的真假,请说明理由.
已知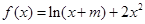 在点
在点 处的切线方程与直线
处的切线方程与直线 垂直.
垂直.
(Ⅰ)若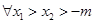 ,
,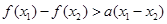 恒成立,求实数
恒成立,求实数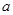 的取值范围.
的取值范围.
(Ⅱ)当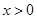 时,求证:
时,求证: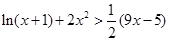 .
.
设函数 ,数列
,数列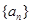 满足
满足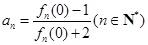
(Ⅰ)求数列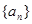 的通项公式;
的通项公式;
(Ⅱ)记 试比较
试比较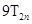 与Q的大小关系,并说明理由.
与Q的大小关系,并说明理由.
下图是一几何体的直观图、主视图、俯视图、左视图.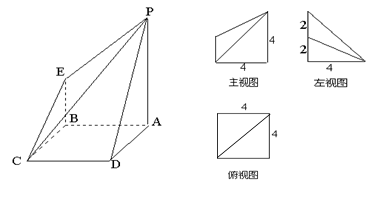
(Ⅰ)若 为
为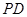 的中点,求证:
的中点,求证: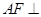 面
面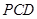 ;
;
(Ⅱ)证明: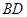 ∥面
∥面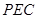 ;
;
(Ⅲ)求面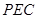 与面
与面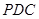 所成的二面角(锐角)的余弦值.
所成的二面角(锐角)的余弦值.
山东省实验中学为了活跃师生的课外文化生活,在2015年3月中旬举办了一次知识竞赛,经过层层筛选,最后五名同学进入了总决赛.在进行笔答题知识竞赛中,最后一个大题是选做题,要求参加竞赛的五名选手从2道题中选做一道进行解答,假设这5位选手选做每一题的可能性均为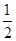 ,求
,求
(Ⅰ)其中甲乙2位选手选做同一道题的概率.
(Ⅱ)设这5位选手中选做第1题的人数为x,求x的分布列及数学期望.