设全集 ,函数
,函数 的定义域为A,函数
的定义域为A,函数 的定义域为B
的定义域为B
(Ⅰ)求集合 与
与 ;
;
(Ⅱ)求 、
、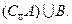
给定项数为
 的数列
的数列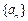 ,其中
,其中
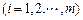 .
.
若存在一个正整数 ,若数列
,若数列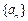 中存在连续的k项和该数列中另一个连续的k项恰好按次序对应相等,则称数列
中存在连续的k项和该数列中另一个连续的k项恰好按次序对应相等,则称数列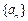 是“k阶可重复数列”,
是“k阶可重复数列”,
例如数列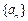

因为 与
与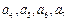 按次序对应相等,所以数列
按次序对应相等,所以数列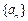 是“4阶可重复数列”.
是“4阶可重复数列”.
(Ⅰ)分别判断下列数列
① ②
②
是否是“5阶可重复数列”?如果是,请写出重复的这5项;
(Ⅱ)若数为 的数列
的数列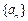 一定是 “3阶可重复数列”,则
一定是 “3阶可重复数列”,则 的最小值是多少?说明理由;
的最小值是多少?说明理由;
(III)假设数列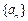 不是“5阶可重复数列”,若在其最后一项
不是“5阶可重复数列”,若在其最后一项 后再添加一项0或1,均可使新数列是“5阶可重复数列”,且
后再添加一项0或1,均可使新数列是“5阶可重复数列”,且 ,求数列
,求数列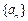 的最后一项
的最后一项 的值.
的值.
一束光线从点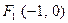 出发,经直线
出发,经直线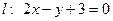 上一点
上一点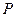 反射后,恰好穿过点
反射后,恰好穿过点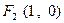 .(Ⅰ)求点
.(Ⅰ)求点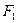 关于直线
关于直线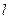 的对称点
的对称点 的坐标;
的坐标;
(Ⅱ)求以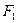 、
、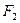 为焦点且过点
为焦点且过点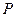 的椭圆
的椭圆 的方程;
的方程;
(Ⅲ)设直线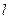 与椭圆
与椭圆 的两条准线分别交于
的两条准线分别交于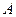 、
、 两点,点
两点,点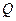 为线段
为线段 上的动点,求点
上的动点,求点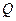 到
到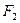 的距离与到椭圆
的距离与到椭圆 右准线的距离之比的最小值,并求取得最小值时点
右准线的距离之比的最小值,并求取得最小值时点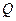 的坐标.
的坐标.
已知函数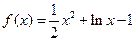 .
.
(1)求函数 在区间
在区间 (
( 为自然对数的底)上的最大值和最小值;
为自然对数的底)上的最大值和最小值;
(2)求证:在区间 上,函数
上,函数 的图象在函数
的图象在函数 的图象的下方;
的图象的下方;
(3)求证: ≥
≥
 .
.
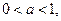 下列不等式一定成立的是()
下列不等式一定成立的是()
A. ; ; |
B.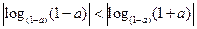 ; ; |
C. ; ; |
D. |