某营养师要为某个儿童预定午餐和晚餐。已知一个单位的午餐含12个单位的碳水化合物6个单位蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素C.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预定多少个单位的午餐和晚餐?
已知函数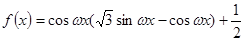 (
(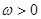 )的周期为
)的周期为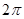 .
.
(Ⅰ)求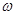 的值及
的值及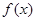 的解析式;
的解析式;
(Ⅱ)在△ABC中,角A,B,C的对边分别是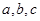 ,且满足
,且满足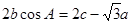 ,
,
求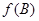 的值.
的值.
已知函数
(Ⅰ)当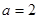 ,且
,且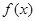 是
是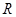 上的增函数,求实数
上的增函数,求实数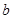 的取值范围;;
的取值范围;;
(Ⅱ)当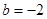 ,且对任意
,且对任意 ,关于
,关于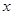 的方程
的方程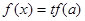 总有三个不相等的实数根,求实数
总有三个不相等的实数根,求实数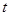 的取值范围.
的取值范围.
已知 分别是椭圆
分别是椭圆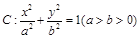 的左、右顶点,点
的左、右顶点,点 在椭圆
在椭圆 上,且直线
上,且直线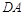 与直线
与直线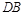 的斜率之积为
的斜率之积为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)如图,已知 是椭圆
是椭圆 上不同于顶点的两点,直线
上不同于顶点的两点,直线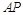 与
与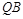 交于点
交于点 ,直线
,直线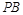 与
与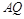 交于点
交于点 .若弦
.若弦 过椭圆的右焦点
过椭圆的右焦点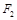 ,求直线
,求直线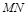 的方程.
的方程.
如图,四棱锥 的底面是直角梯形,
的底面是直角梯形,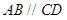 ,
, ,
, 和
和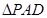
是两个边长为2的正三角形,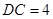 ,
, 为
为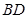 的中点,
的中点,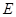 为
为 的中点.
的中点.
(Ⅰ)求证: ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
若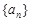 是各项均不为零的等差数列,公差为
是各项均不为零的等差数列,公差为 ,
, 为其前
为其前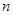 项和,且满足
项和,且满足 ,
, .数列
.数列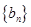 满足
满足 ,
,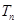 为数列
为数列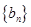 的前
的前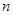 项和.
项和.
(Ⅰ)求 和
和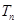 ;
;
(Ⅱ)是否存在正整数 ,使得
,使得 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有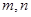 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.