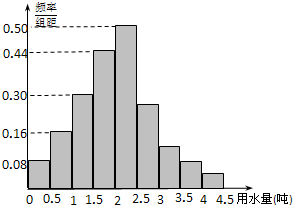
（本小题满分10分）某地区100位居民的人均月用水量（单位：t）的频率分布直方图及频数分布表如下：
| 分组 |
频数 |
| [0，0．5） |
4 |
| [0．5，1） |
8 |
| [1，1．5） |
15 |
| [1．5，2） |
22 |
| [2，2．5） |
25 |
| [2．5，3） |
14 |
| [3，3．5） |
6 |
| [3．5，4） |
4 |
| [4，4．5] |
2 |
| 合计 |
100 |
（1）根据频率分布直方图估计这组数据的众数与平均数；
（2）当地政府制定了人均月用水量为3t的标准，若超出标准加倍收费，当地政府解释说，85%以上的居民不超出这个标准，这个解释对吗？为什么？
(本题12分) 已知函数
在
上为增函数，在[
0,2]上为减函数，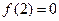
。
(1)求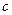
的值；
(2)求证: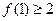
。
(本题12分)某商场为吸引顾客消费推出一项优惠活动．活动规则如下：消费
额每满100元可转动如图所示的转盘一次，并获得相应金额的返券，假定指针等可能地停在任一位置． 若指针停在A区域返券60元；停在B区域返券30元；停在C区域不返券． 例如：消费218元，可转动转盘2次，所获得的返券金额是两次金额之和．
（1）若某位顾客消费128元，求返券金额不低于30元的概率；
（2）若某位顾客恰好消费280元，并按规则参与了活动，他获得返券的金额记为
（元）．求随机变量的分布列和数学期望．
(本题12分)已知二
项式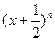
的展开式中前三项的系数成等差数列．
(1)求
的值;
(2)设
.
①求
的值;②求
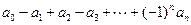的值;
③求
的最大值.
(本题12分)某班从4名男同学和2名女同学中任选3人参加全校举行的“八荣八耻”教育演讲赛。如果设随机变量
表示所选3人中女同学的人数.
(1)若
,求共有不同选法的种数;
(2)求的分布列和数学期望；
(3)求“
”的概率。
设函数
，
.
(1)当
时，求与函数
图象相切且与直线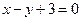
平行的直线方程
(2)求函数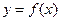
的单调区间
(3)是否存在正实数
，使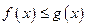
对一切正实数
都成立？若存在，求出的取值范围；若不存在，请说明理由.