(本题12分)某班从4名男同学和2名女同学中任选3人参加全校举行的“八荣八耻”教育演讲赛。如果设随机变量 表示所选3人中女同学的人数.
表示所选3人中女同学的人数.
(1)若 ,求共有不同选法的种数;
,求共有不同选法的种数;
(2)求 的分布列和数学期望;
的分布列和数学期望;
(3)求“ ”的概率。
”的概率。
已知函数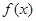 的定义域
的定义域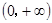 ,若
,若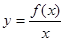 在
在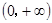 上为增函数,则称
上为增函数,则称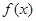 为“一阶比增函数”;若
为“一阶比增函数”;若 在
在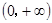 上为增函数,则称
上为增函数,则称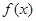 为“二阶比增函数”。把所有由“一阶比增函数”组成的集合记为
为“二阶比增函数”。把所有由“一阶比增函数”组成的集合记为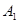 ,把所有由“二阶比增函数”组成的集合记为
,把所有由“二阶比增函数”组成的集合记为 .
.
(1)已知函数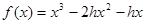 ,若
,若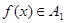 且
且 ,求实数
,求实数 的取值范围;
的取值范围;
(2)已知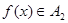 ,且存在常数
,且存在常数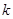 ,使得对任意的
,使得对任意的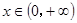 ,都有
,都有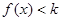 ,求
,求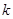 的最小值.
的最小值.
已知椭圆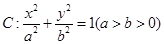 的离心率为
的离心率为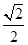 ,其左,右焦点分别为
,其左,右焦点分别为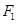 ,
, ,点
,点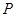 是坐标平面内一点,且
是坐标平面内一点,且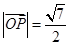 ,
,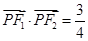 ,其中
,其中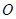 为坐标原点.
为坐标原点.
(1)求椭圆 的方程;
的方程;
(2)过点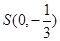 ,且斜率为
,且斜率为 的动直线
的动直线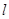 交椭圆于
交椭圆于 两点,在
两点,在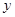 轴上是否存在定点
轴上是否存在定点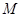 ,使以
,使以 为直径的圆恒过这个定点?若存在,求出点
为直径的圆恒过这个定点?若存在,求出点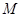 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
如图,在多面体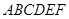 中,
中,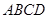 为菱形,
为菱形,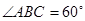 ,
,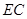
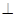 平面
平面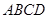 ,
,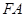
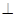 平面
平面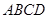 ,
,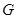 为
为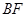 的中点,若
的中点,若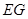
 平面
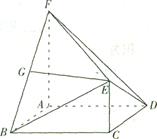
平面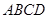 .
.
(1)求证: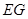
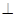 平面
平面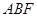 ;
;
(2)若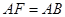 ,求二面角
,求二面角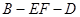 的余弦值.
的余弦值.
甲箱子里装有3个白球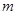 个黑球,乙箱子里装有
个黑球,乙箱子里装有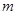 个白球,2个黑球,在一次试验中,分别从这两个箱子里摸出一个球,若它们都是白球,则获奖
个白球,2个黑球,在一次试验中,分别从这两个箱子里摸出一个球,若它们都是白球,则获奖
(1) 当获奖概率最大时,求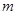 的值;
的值;
(2)在(1)的条件下,班长用上述摸奖方法决定参加游戏的人数,班长有4次摸奖机会(有放回摸取),当班长中奖时已试验次数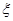 即为参加游戏人数,如4次均未中奖,则
即为参加游戏人数,如4次均未中奖,则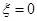 ,求
,求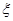 的分布列和
的分布列和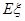 .
.
 中,内角
中,内角 的对边分别是
的对边分别是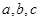 ,已知
,已知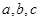 成等比数列,且
成等比数列,且 .
.
(1)求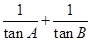 的值;
的值;
(2)设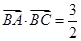 ,求
,求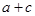 的值.
的值.