(本小题满分12分)在2015年全运会上两名射击运动员甲、乙在比赛中打出如下成绩:
甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;
乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;
(1)用茎叶图表示甲、乙两人的成绩;并根据茎叶图估计他们的中位数;
(2)已知甲、乙两人成绩的方差分别为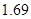 与
与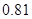 ,分别计算两个样本的平均数
,分别计算两个样本的平均数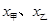 和标准差
和标准差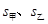 ,并根据计算结果估计哪位运动员的成绩比较好,哪位运动员的成绩比较稳定.
,并根据计算结果估计哪位运动员的成绩比较好,哪位运动员的成绩比较稳定.
选修4—4:坐标系与参数方程
在直角坐标系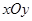 中,圆
中,圆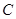 的参数方程
的参数方程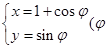 为参数).以
为参数).以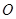 为极点,
为极点,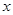 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆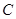 的极坐标方程;
的极坐标方程;
(Ⅱ)直线 的极坐标方程是
的极坐标方程是 ,射线
,射线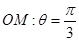 与圆
与圆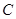 的交点为
的交点为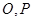 ,与直
,与直
线 的交点为
的交点为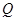 ,求线段
,求线段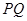 的长.
的长.
(本小题满分10分)选修4-1:几何证明选讲
如图, 四点在同一圆上,
四点在同一圆上,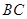 与
与 的延长线交于点
的延长线交于点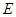 ,点
,点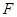 在
在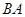 的延长线上.
的延长线上.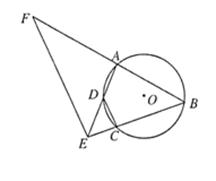
(1)若 ,
,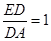 ,求
,求 的值;
的值;
(2)若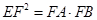 ,证明:
,证明: .
.
已知函数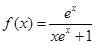 .
.
(1)证明: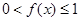 ;
;
(2)当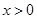 时,
时,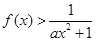 ,求
,求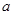 的取值范围.
的取值范围.
已知椭圆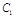 :
: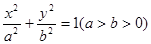 的离心率为
的离心率为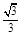 ,直线
,直线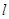 :
: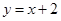 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆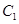 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.
(1)求椭圆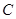 的方程;
的方程;
(2)过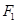 的直线
的直线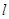 交椭圆
交椭圆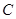 于
于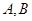 两点,则
两点,则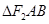 的内切圆的面积是否存在最大值,若存在其最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值,若存在其最大值及此时的直线方程;若不存在,请说明理由.
如图所示,在四棱锥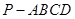 中,底面四边形
中,底面四边形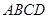 是菱形,
是菱形,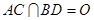 ,
,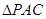 是边长为2的等边三角形,
是边长为2的等边三角形,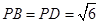 ,
,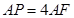 .
.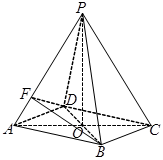
(1)求证: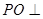 底面
底面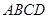 ;
;
(2)求直线 与平面
与平面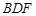 所成角的大小;
所成角的大小;
(3)在线段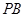 上是否存在一点
上是否存在一点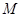 ,使得
,使得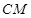 ∥平面
∥平面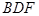 ?如果存在,求
?如果存在,求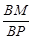 的值,如果不存在,请说明理由.
的值,如果不存在,请说明理由.