((本小题满分10分)选修4—1:几何证明选讲
如图,已知AD是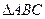 的外角
的外角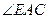 的平分线,交BC的延长线于点D,延长DA交
的平分线,交BC的延长线于点D,延长DA交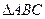 的外接圆于点F,连结FB、FC
的外接圆于点F,连结FB、FC
(I)求证:FB=FC;
(II)求证:FB2=FA·FD;
(III)若AB是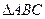 外接圆的直径,
外接圆的直径,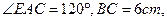 求AD的长。
求AD的长。
((本小题满分12分)
设函数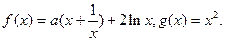
(I)若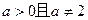 ,直线l与函数
,直线l与函数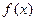 和函数
和函数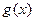 的图象相切于一点,求切线l的方程。
的图象相切于一点,求切线l的方程。
(II)若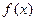 在[2,4]内为单调函数,求实数a的取值范围;
在[2,4]内为单调函数,求实数a的取值范围;
((本小题满分12分)
椭圆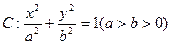 的两个焦点F1、F2,点P在椭圆C上,且PF1⊥F1F2,且|PF1|=
的两个焦点F1、F2,点P在椭圆C上,且PF1⊥F1F2,且|PF1|=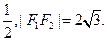
(I)求椭圆C的方程。
(II)以此椭圆的上顶点B为直角顶点作椭圆的内接等腰直角三角形ABC,这样的直角三角形是否存在?若存在,请说明有几个;若不存在,请说明理由。
((本小题满分12分)
在边长为5的菱形ABCD中,AC=8。现沿对角线BD把△ABD折起,折起后使∠ADC的余弦值为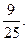
(I)求证:平面ABD⊥平面CBD;
(II)若M是AB的中点,求折起后AC与平面MCD所成角的一个三角函数值.
(本小题满分12分)
随机抽取某中学甲乙两个班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图(中间的数字表示身高的百位、十位,旁边的数字分别表示身高的个位数)如图所示。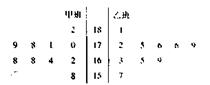
(I)根据茎叶图判断哪个班的平均身高较高;
(II)计算甲班的样本方差;
(III)现从乙班这10名同学中随机抽取两名身高不低于175cm的同学,求身高为176cm的同学被抽中的概率。