某市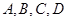 四所中学报名参加某高校今年自主招生的学生人数如下表所示:
四所中学报名参加某高校今年自主招生的学生人数如下表所示:
| 中学 |
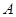 |
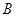 |
 |
 |
| 人数 |
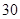 |
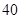 |
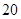 |
 |
为了了解参加考试的学生的学习状况,该高校采用分层抽样的方法从报名参加考试的四所中学的学生当中随机抽取50名参加问卷调查.
(1)问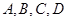 四所中学各抽取多少名学生?
四所中学各抽取多少名学生?
(2)在参加问卷调查的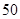 名学生中,从来自
名学生中,从来自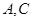 两所中学的学生当中随机抽取两名学生,用
两所中学的学生当中随机抽取两名学生,用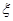 表示抽得
表示抽得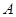 中学的学生人数,求
中学的学生人数,求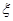 的分布列,数学期望和方差.
的分布列,数学期望和方差.
已知函数f(x)=|x+1|,g(x)=2|x|+a.
(1)当a=0时,解不等式f(x)≥g(x);
(2)若任意x∈R,f(x) g(x)恒成立,求实数a的取值范围.
g(x)恒成立,求实数a的取值范围.
已知函数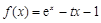 (e为自然对数的底数).
(e为自然对数的底数).
(1)求函数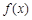 的单调增区间;
的单调增区间;
(2)设不等式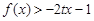 的解集为M,且集合
的解集为M,且集合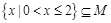 ,求实数t的取值范围.
,求实数t的取值范围.
已知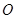 是
是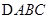 内任意一点,连结
内任意一点,连结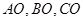 并延长交对边于
并延长交对边于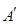 ,
,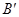 ,
,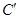 ,则
,则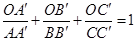 .这是平面几何的一个命题,其证明常常采用“面积法”:
.这是平面几何的一个命题,其证明常常采用“面积法”: 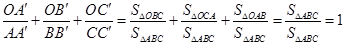 .
.
运用类比,猜想对于空间中的四面体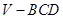 ,存在什么类似的结论,并用“体积法”证明。
,存在什么类似的结论,并用“体积法”证明。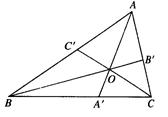
已知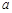 为实数,函数
为实数,函数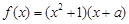 .
.
(1) 若 ,求函数
,求函数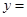
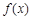 在[-
在[-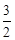 ,1]上的极大值和极小值;
,1]上的极大值和极小值;
(2)若函数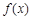 的图象上有与
的图象上有与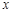 轴平行的切线,求
轴平行的切线,求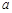 的取值范围.
的取值范围.
设函数 .
.
(1)求不等式 的解集;
的解集;
(2)若不等式 的解集是非空的集合,求实数
的解集是非空的集合,求实数 的取值范围.
的取值范围.