已知 是椭圆
是椭圆 的左,右顶点,
的左,右顶点, ,过椭圆C的右焦点
,过椭圆C的右焦点 的直线交椭圆于点
的直线交椭圆于点 ,交直线
,交直线 于点
于点 ,且直线
,且直线 的斜率成等差数列,
的斜率成等差数列, 是椭圆上的两动点,
是椭圆上的两动点, 的横坐标之和为2,
的横坐标之和为2, 的中垂线交
的中垂线交 轴于
轴于 点
点
(1)求椭圆 的方程;(2)求△
的方程;(2)求△ 的面积的最大值
的面积的最大值
本小题满分12分)
如图,在四棱柱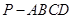 中,底面
中,底面 为直角梯形,
为直角梯形, ,
,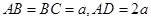 ,
,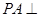 平面
平面 ,
,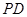 与平面
与平面 成
成 角.
角.
(Ⅰ)若 ,
, 为垂足,求证:
为垂足,求证:
(Ⅱ)求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
(本小题满分12分)
如图8—3,已知ΔOFQ的面积为S,且 .(1)若
.(1)若 ,求向量
,求向量 与
与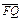 的夹角θ的取值范围;(2)设
的夹角θ的取值范围;(2)设 ,
, ,若以O为中心,F为焦点的椭圆经过点Q,当
,若以O为中心,F为焦点的椭圆经过点Q,当 取得最小值时,求此椭圆方程.
取得最小值时,求此椭圆方程.
(本小题满分12分)
从集合 的所有非空子集中,等可能地取出一个.
的所有非空子集中,等可能地取出一个.
(1)记性质r:集合中的所有元素之和为10,求所取出的非空子集满足性质r的概率;
(2)记所取出的非空子集的元素个数为 ,求
,求 的分布列和数学期望E
的分布列和数学期望E .
.
(本小题满分12分)
数列 中,
中,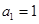 ,且点
,且点 在直线
在直线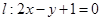 上.
上.
(Ⅰ)设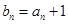 ,求证:
,求证: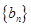 是等比数列;
是等比数列;
(Ⅱ)设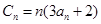 ,求
,求 的前
的前 项和.
项和.
(本题满分12分)
已知函数 .
.
(1)求 在
在 上的最大值;
上的最大值;
(2)若对任意的实数 ,不等式
,不等式 恒成立,求实数
恒成立,求实数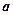 的取值范围;
的取值范围;
(3)若关于 的方程
的方程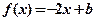 在
在 上恰有两个不同的实根,求实数
上恰有两个不同的实根,求实数 的取值范围.
的取值范围.