(本小题满分14分)如图,在直三棱柱ABC—A1B1C1中, ,
,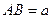 ,
,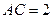 ,
,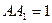 ,点D在棱
,点D在棱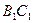 上,且
上,且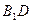 ∶
∶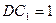 ∶3 w.
∶3 w. 
 (1)证明:无论a为任何正数,均有BD⊥A1C;
(1)证明:无论a为任何正数,均有BD⊥A1C;
(2)当a为何值时,二面角B—A1D—B1为60°?
(本小题满分14分)椭圆 的两个焦点F1、F2,点P在椭圆C上,且P F1⊥PF2,,| P F1|=
的两个焦点F1、F2,点P在椭圆C上,且P F1⊥PF2,,| P F1|=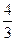 | ,P F2|=
| ,P F2|=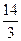 .
.
(I)求椭圆C的方程;
(II)若直线L过圆x2+y2+4x-2y=0的圆心M交椭圆于A、B两点,且A、B关于点M对称,求直线L的方程。
(本小题满分13分)
某港口要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口的O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.
(I)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(II)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值.
(本小题满分13分)
如图,在三棱锥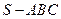 中,侧面
中,侧面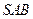
与侧面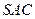 均为等边三角形,
均为等边三角形,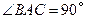 ,
,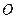 为
为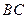 中点.
中点.
(Ⅰ)证明: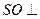 平面
平面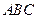 ;
;
(Ⅱ)求二面角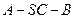 的余弦值.
的余弦值.
(本题13分)已知函数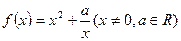
(1)判断函数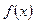 的奇偶性;
的奇偶性;
(2)若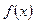 在区间
在区间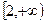 是增函数,求实数
是增函数,求实数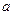 的取值范围。
的取值范围。
(本题13分)记关于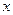 的不等式
的不等式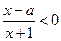 的解集为
的解集为 ,不等式
,不等式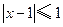 的解集为
的解集为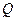 .
.
(1)若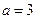 ,求
,求 ;
;
(2)若 ,求正数
,求正数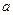 的取值范围.
的取值范围.