(本小题满分12分)二次函数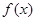 满足
满足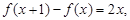 且
且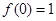 .
.
(1)求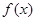 的解析式;
的解析式;
(2)在区间 上,
上,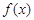 的图象恒在
的图象恒在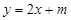 的图象上方,试确定实数m的范围.
的图象上方,试确定实数m的范围.
已知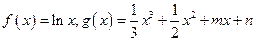 ,直线
,直线 与函数
与函数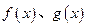 的图象都相切于点
的图象都相切于点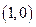 .
.
(1)求直线 的方程及
的方程及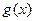 的解析式;
的解析式;
(2)若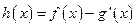 (其中
(其中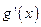 是
是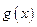 的导函数),求函数
的导函数),求函数 的值域.
的值域.
某种家用电器每台的销售利润与该电器的无故障使用时间T (单位:年)有关.若T≤1,则销售利润为0元;若1<T≤3,则销售利润为100元;若T>3,则销售利润为200元.设每台该种电器的无故障使用时间T≤1,1<T≤3及T>3这三种情况发生的概率分别为p1,p2,p3,又知p1,p2是方程 的两个根,且p2=p3.
的两个根,且p2=p3.
(1)求p1,p2,p3的值;
(2)记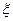 表示销售两台这种家用电器的销售利润总和,求
表示销售两台这种家用电器的销售利润总和,求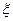 的期望.
的期望.
设 是定义在[-1,1]上的偶函数,
是定义在[-1,1]上的偶函数, 的图象与
的图象与 的图象关于直线
的图象关于直线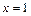 对称,且当x∈[ 2,3 ] 时,
对称,且当x∈[ 2,3 ] 时,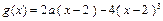 222233.(1)求
222233.(1)求 的解析式;(2)若
的解析式;(2)若 在
在 上为增函数,求
上为增函数,求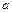 的取值范围;(3)是否存在正整数
的取值范围;(3)是否存在正整数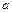 ,使
,使 的图象的最高点落在直线
的图象的最高点落在直线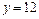 上?若存在,求出
上?若存在,求出 的值;若不存在,请说明理由
的值;若不存在,请说明理由
(本小题满分12分)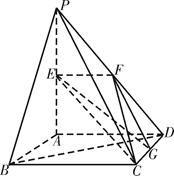 如图,平面
如图,平面 平面ABCD,
平面ABCD,
ABCD为正方形, 是直角三角形,
是直角三角形,
且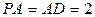 ,E、F、G分别是
,E、F、G分别是
线段PA,PD,CD的中点.
(1)求证: ∥面EFC;
∥面EFC;
(2)求异面直线EG与BD所成的角;
(3)在线段CD上是否存在一点Q,
使得点A到面EFQ的距离为0.8. 若存在,
求出CQ的值;若不存在,请说明理由.
(本小题满分12分)甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在7,8,9,10环,且每次射击成绩互不影响.射击环数的频率分布条形图如下: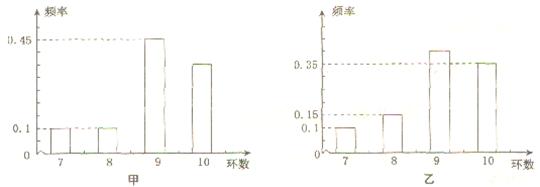
若将频率视为概率,回答下列问题.(Ⅰ)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率; (Ⅱ)若甲、乙两运动员各自射击1次,ξ表示这2次射击中击中9环以上(含9环)的次数,求ξ的分布列及Eξ.