(本小题满分12分)甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在7,8,9,10环,且每次射击成绩互不影响.射击环数的频率分布条形图如下: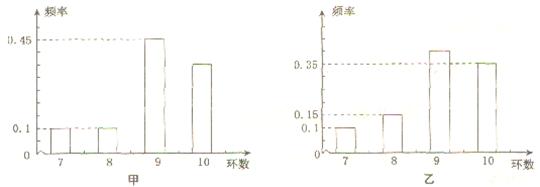
若将频率视为概率,回答下列问题.(Ⅰ)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率; (Ⅱ)若甲、乙两运动员各自射击1次,ξ表示这2次射击中击中9环以上(含9环)的次数,求ξ的分布列及Eξ.
(本小题满分14分)
已知函数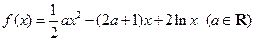 .
.
(Ⅰ)若曲线 在
在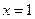 和
和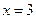 处的切线互相平行,求
处的切线互相平行,求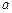 的值;
的值;
(Ⅱ)求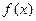 的单调区间;
的单调区间;
(Ⅲ)设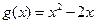 ,若对任意
,若对任意 ,均存在
,均存在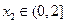 ,使得
,使得 ,求
,求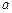 的取值范围.
的取值范围.
(本小题满分13分)
已知椭圆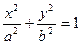 (
(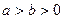 )的右焦点为
)的右焦点为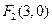 ,离心率为
,离心率为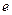 .
.
(Ⅰ)若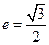 ,求椭圆的方程;
,求椭圆的方程;
(Ⅱ)设直线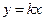 与椭圆相交于
与椭圆相交于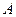 ,
,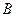 两点,
两点,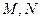 分别为线段
分别为线段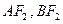 的中点. 若坐标原点
的中点. 若坐标原点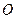 在以
在以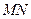 为直径的圆上,且
为直径的圆上,且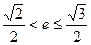 ,求
,求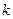 的取值范围.
的取值范围.
(本小题满分13分)
一个袋中装有 个形状大小完全相同的小球,球的编号分别为
个形状大小完全相同的小球,球的编号分别为 .
.
(Ⅰ)若从袋中每次随机抽取1个球,有放回的抽取2次,求取出的两个球编号之和为6的概率;
(Ⅱ)若从袋中每次随机抽取 个球,有放回的抽取3次,求恰有
个球,有放回的抽取3次,求恰有 次抽到
次抽到 号球的概率;
号球的概率;
(Ⅲ)若一次从袋中随机抽取 个球,记球的最大编号为
个球,记球的最大编号为 ,求随机变量
,求随机变量 的分布列.
的分布列.
(本小题满分13分)
如图,在三棱柱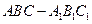 中,侧面
中,侧面 ,
,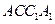 均为正方形,∠
均为正方形,∠ ,点
,点 是棱
是棱 的中点.
的中点.
(Ⅰ)求证: ⊥平面
⊥平面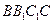 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求二面角 的余弦值.
的余弦值.
(本小题满分13分)
已知函数 .
.
(Ⅰ)若点 在角
在角 的终边上,求
的终边上,求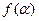 的值;
的值;
(Ⅱ)若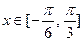 ,求
,求 的值域.
的值域.