(本小题满分14分)
已知函数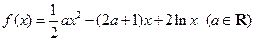 .
.
(Ⅰ)若曲线 在
在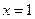 和
和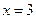 处的切线互相平行,求
处的切线互相平行,求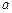 的值;
的值;
(Ⅱ)求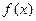 的单调区间;
的单调区间;
(Ⅲ)设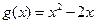 ,若对任意
,若对任意 ,均存在
,均存在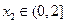 ,使得
,使得 ,求
,求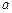 的取值范围.
的取值范围.
(本小题满分13分)已知函数 ,方程
,方程 在
在 上的解按从小到大的顺序排成数列
上的解按从小到大的顺序排成数列
 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,数列
,数列 的前
的前 项和为
项和为 ,求
,求 的表达式.
的表达式.
(本小题满分13分)甲、乙、丙三人参加某次招聘会,若甲应聘成功的概率为 ,乙、丙应聘成功的概率均为
,乙、丙应聘成功的概率均为 ,且三人是否应聘成功是相互独立的.
,且三人是否应聘成功是相互独立的.
(Ⅰ)若甲、乙、丙都应聘成功的概率是 ,求
,求 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,设 表示甲、乙两人中被聘用的人数,求
表示甲、乙两人中被聘用的人数,求 的数学期望.
的数学期望.
设 均为正数,且 .
证明:
(Ⅰ)若
,则
;
(Ⅱ)
是
的充要条件.
选修4-4:坐标系与参数方程
在直角坐标系
中,曲线
(
为参数,且
),其中
,在以
为极点,
轴正半轴为极轴的极坐标系中,曲线
(Ⅰ)求
与
交点的直角坐标;
(Ⅱ)若
与
相交于点
,
与
相交于点
,求
最大值.
如图
是等腰三角形
内一点,圆
与
的底边
交于
两点,与底边上的高交于点
,且与
分别相切于
两点.
(Ⅰ)证明
(Ⅱ)若 等于圆 半径,且 ,求四边形 的面积.