设 是定义在[-1,1]上的偶函数,
是定义在[-1,1]上的偶函数, 的图象与
的图象与 的图象关于直线
的图象关于直线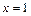 对称,且当x∈[ 2,3 ] 时,
对称,且当x∈[ 2,3 ] 时,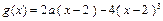 222233.(1)求
222233.(1)求 的解析式;(2)若
的解析式;(2)若 在
在 上为增函数,求
上为增函数,求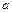 的取值范围;(3)是否存在正整数
的取值范围;(3)是否存在正整数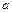 ,使
,使 的图象的最高点落在直线
的图象的最高点落在直线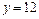 上?若存在,求出
上?若存在,求出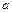 的值;若不存在,请说明理由
的值;若不存在,请说明理由
(本小题满分12分)
已知函数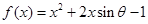 ,
,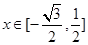
(1)当 时,求
时,求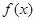 的最大值和最小值
的最大值和最小值
(2)若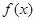 在
在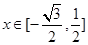 上是单调函数,且
上是单调函数,且 ,求
,求 的取值范围
的取值范围
(本小题满分10分)
如图: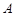 、
、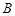 是单位圆
是单位圆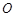 上的点,
上的点,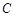 是圆与
是圆与 轴正半轴的交点,三角形
轴正半轴的交点,三角形 为正三角形,且AB∥
为正三角形,且AB∥ 轴.
轴.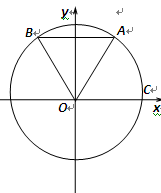
(1)求 的三个三角函数值;
的三个三角函数值;
(2)求 及
及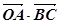 .
.
设数列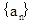 满足:
满足: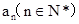 是整数,且
是整数,且 是关于x的方程
是关于x的方程 的根.
的根.
(1)若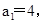 且n≥2时,
且n≥2时,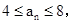 求数列{an}的前100项和S100;
求数列{an}的前100项和S100;
(2)若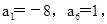 且
且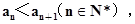 求数列
求数列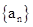 的通项公式.
的通项公式.
已知⊙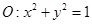 和点
和点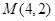 .
.
(Ⅰ)过点 向⊙
向⊙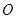 引切线
引切线 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)求以点 为圆心,且被直线
为圆心,且被直线 截得的弦长为4的⊙
截得的弦长为4的⊙ 的方程;
的方程;
(Ⅲ)设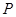 为(Ⅱ)中⊙
为(Ⅱ)中⊙ 上任一点,过点
上任一点,过点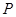 向⊙
向⊙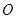 引切线,切点为
引切线,切点为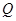 . 试探究:平面内是否存在一定点
. 试探究:平面内是否存在一定点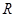 ,使得
,使得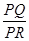 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
设二次函数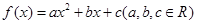 满足下列条件:
满足下列条件:
①当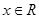 时,
时, 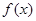 的最小值为0,且
的最小值为0,且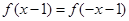 恒成立;
恒成立;
②当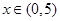 时,
时,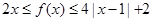 恒成立.
恒成立.
(I)求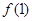 的值;
的值;
(Ⅱ)求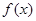 的解析式;
的解析式;
(Ⅲ)求最大的实数m(m>1),使得存在实数t,只要当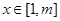 时,就有
时,就有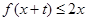 成立
成立