已知椭圆 ,离心率为
,离心率为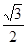 ,两焦点分别为
,两焦点分别为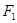 、
、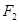 ,过
,过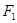 的直线交椭圆
的直线交椭圆 于
于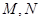 两点,且△
两点,且△ 的周长为
的周长为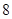 .
.
(1)求椭圆 的方程;
的方程;
(2)过点
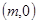 作圆
作圆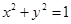 的切线
的切线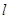 交椭圆
交椭圆 于
于 两点,求弦长
两点,求弦长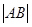 的最大值.
的最大值.
某食品厂定期购买面粉,已知该厂每天需要面粉6吨,每吨面粉的价格为3200元,面粉的保管等其它费用为平均每吨每天3元,购买面粉每次需要 支付运费900元。
支付运费900元。
(Ⅰ)求该厂每隔多少天购买一次面粉,才能使平均每天支付的总费用 最少?最少费用为多少?
最少?最少费用为多少?
(Ⅱ)某提供面粉的公司规定:当一次购买面粉不少于120吨时,价格可享受9.5折优惠,问该厂是否考虑利用此优惠条件?请说明理由。
制定投资计划时,不仅要考虑可能获得的赢利,而且要考虑可能出现的亏损。某投资人打算投资甲、乙两个项目,根据预测,甲、乙项目可能的最大赢利率分别为100%和50%,可能的最大亏损率分别为30%和10%,投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元,问投资人对甲、乙两个项目各投资多少万元,才能使可能的赢利最大?
已知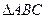
 中,
中,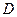 为边
为边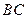 上的一点,
上的一点,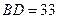 ,
,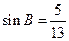 ,
,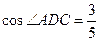 ,求
,求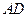 .
.
已知数列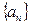 为等差数列,其中
为等差数列,其中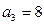 ,
,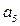 恰为
恰为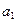 和
和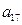 的等比中项。
的等比中项。
(Ⅰ)求数列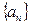 的通项公式
的通项公式 ;
;
(Ⅱ)若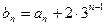 ,求数列
,求数列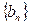 的前n项和
的前n项和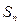 。
。
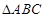 中,
中,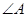 、
、 、
、 所对的边分别为
所对的边分别为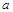 、
、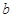 、
、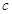
(Ⅰ) 若
若 、
、 、
、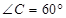 ,求
,求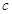 .
. (Ⅱ)若
(Ⅱ)若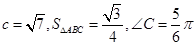 ,
,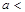
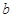 ,求
,求 、
、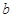 。
。