已知函数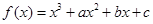 在
在 与
与 时都取得极值.
时都取得极值.
(1)求 的值及
的值及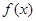 的极大值与极小值;
的极大值与极小值;
(2)若方程 有三个互异的实根,求
有三个互异的实根,求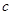 的取值范围;
的取值范围;
(3)若对 ,不等式
,不等式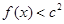 恒成立,求
恒成立,求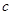 的取值范围.
的取值范围.
如图: 在 中,角
中,角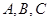 的对边分别为
的对边分别为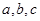

(Ⅰ) 若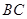 边上的中点为
边上的中点为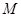 ,且
,且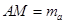 ,
,
求证: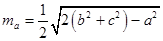 ;
;
(Ⅱ) 若 是锐角三角形,且
是锐角三角形,且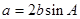 .
.
求 的取值范围.
的取值范围.
数列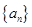 满足
满足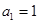 ,
, (
(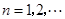 ),
),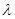 是常数.
是常数.
(Ⅰ)当 时,求
时,求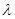 及
及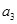 的值;
的值;
(Ⅱ)数列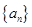 是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由.
是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由.
已知函数 是
是 上的增函数,
上的增函数,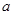 ,
,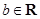 .
.
(Ⅰ)若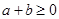 ,求证:
,求证: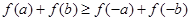 ;
;
(Ⅱ)判断(Ⅰ)中命题的逆命题是否成立,并证明你的结论.
在对人们的休闲方式的一次调查中,共调查了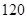 人,其中女性
人,其中女性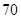 人,男性
人,男性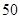 人.女性中有
人.女性中有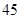 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外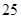 人主要的休闲方式是运动;男性中有
人主要的休闲方式是运动;男性中有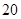 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外 人主要的休闲方式是运动.
人主要的休闲方式是运动.
(1)根据以上数据建立一个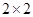 的列联表;
的列联表;
(2)判断性别与休闲方式是否有关系.
在数列{an}中, ,试猜想这个数列的通项公式。
,试猜想这个数列的通项公式。