已知椭圆 的方程为
的方程为 ,双曲线
,双曲线 的左、右焦点分别是
的左、右焦点分别是 的左、右顶点,而
的左、右顶点,而 的
的
左、右顶点分别是 的左、右焦点.
的左、右焦点.
(1)求双曲线 的方程;
的方程;
(2)若直线 与双曲线
与双曲线 恒有两个不同的交点A和B,且
恒有两个不同的交点A和B,且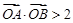 (其中
(其中 为原点),求实数
为原点),求实数 的范围.
的范围.
某单位从一所学校招收某类特殊人才.对 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
 |
一般 |
良好 |
优秀 |
| 一般 |
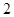 |
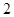 |
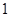 |
| 良好 |
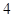 |
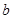 |
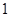 |
| 优秀 |
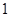 |
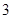 |
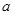 |
例如表中运动协调能力良好且逻辑思维能力一般的学生是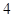 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这 位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为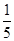 .
.
(1)求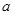 ,
,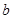 的值;
的值;
(2)从运动协调能力为优秀的学生中任意抽取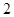 位,求其中至少有一位逻辑思维能力优秀的学生的概率.
位,求其中至少有一位逻辑思维能力优秀的学生的概率.
已知函数 .
.
(1)求 的值及函数
的值及函数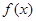 的单调递增区间;
的单调递增区间;
(2)求函数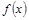 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
从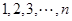 中这
中这 个数中取
个数中取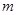 (
( ,
, )个数组成递增等差数列,所有可能的递增等差数列的个数记为
)个数组成递增等差数列,所有可能的递增等差数列的个数记为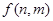 .
.
(1)当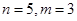 时,写出所有可能的递增等差数列及
时,写出所有可能的递增等差数列及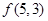 的值;
的值;
(2)求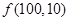 ;
;
(3)求证: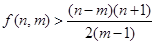 .
.
已知椭圆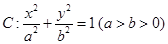 经过点
经过点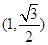 ,离心率为
,离心率为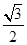 .
.
(1)求椭圆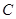 的方程;
的方程;
(2)直线 与椭圆
与椭圆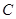 交于
交于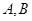 两点,点
两点,点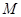 是椭圆
是椭圆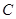 的右顶点.直线
的右顶点.直线 与直线
与直线 分别与
分别与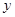 轴交于点
轴交于点 ,试问以线段
,试问以线段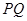 为直径的圆是否过
为直径的圆是否过 轴上的定点?若是,求出定点坐标;若不是,说明理由.
轴上的定点?若是,求出定点坐标;若不是,说明理由.
已知函数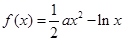 ,
,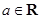 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若函数 在区间
在区间 的最小值为
的最小值为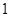 ,求
,求 的值.
的值.