设函数
，若
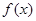在点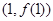
处的切线斜率为
．
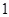（Ⅰ）用
表示
；
（Ⅱ）设
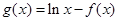，若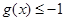
对定义域内的
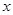恒成立，
（ⅰ）求实数的取值范围；
（ⅱ）对任意的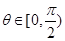
，证明：
．
(本小题满分12分)
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC, △PAD是等边三角形,已知BD=2AD=8,AB=2DC=
(1)设M是PC上的一点,证明：平面MBD⊥平面PAD(2)求四棱锥P-ABCD的体积
(本小题满分12分)
已知数列{an}的前n项和为Sn, Sn+1="4an+2," a1="1," bn=an+1-2an(n∈N*)
(1) 求数列{bn}的前n项和Tn.
(2)求 an
(本小题满分12分)
令函数f(x)=
﹒
,="(2cosx,1)," =(cosx,2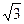
sinxcosx),x∈R
(1)求f(x)的最小正周期与单调增区间
(2)在△ABC中,a,b,c分别是角A,B,C的 对边,已知f(A)=2,b=1,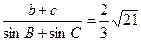
,求△ABC的面积.
椭圆C：
的两个焦点分别为
,
是椭圆上一点，且满足
。
（1）求离心率e的取值范围；
（2）当离心率e取得最小值时，点N( 0 , 3 )到椭圆上的点的最远距离为
。
(i)求此时椭圆C的方程；
(ii)设斜率为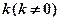
的直线l与椭圆C相交于不同的两点A、B，Q为AB的中点，问A、B两点能否关于过点P（0，
）、Q的直线对称？若能，求出
的取值范围；若不能，请说明理由。
在平面直角坐标系
O
中，直线
与抛物线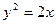
相交于
、
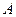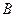两点。
（Ⅰ）求证：“如果直线过点
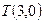，那么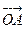
＝
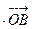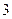”是真命题；
（Ⅱ）写出（1）中命题的逆命题，判断它是真命题还是假命题，并说明理由。