已知:如图,在 中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF.
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.
在Rt△ABC中,已知斜边长c=40,a︰b=3︰4,求两条直角边的长.
小明想知道学校旗杆的高度,他把绳子一端挂在旗杆顶端,发现绳子垂到地面时还余1m;当他把绳子下端拉开5m后,绳子下端刚好接触地面,如图,你能帮他求出旗杆的高度吗?
(1)观察图,并填写下表(图中每个小方格的面积为1单位面积):
 |
A的面积 (单位面积) |
B的面积 (单位面积) |
C的面积 (单位面积) |
| 图① |
|||
| 图② |
(2)三个正方形A,B,C的面积之间有什么关系?
(3)三个正方形围成的一个直角三角形的三边长之间存在什么关系?
如图,△ABC中,∠ACB=90°,AC=9,BC=12,求Rt△ABC中斜边AB上的高CD.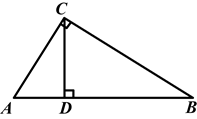
《中华人民共和国道路交通安全法》规定:小汽车在城市道路上行驶速度不得超过70km/h.如图,一辆小汽车在一条城市道路上直道行驶,某一时刻刚好行驶到路对面车速检测仪(点A)的正前方30m处(点C),过了2s后,测得小汽车与车速检测仪间的距离AB为50m.这辆小汽车超速了吗?