(1)观察图,并填写下表(图中每个小方格的面积为1单位面积):
 |
A的面积 (单位面积) |
B的面积 (单位面积) |
C的面积 (单位面积) |
| 图① |
|
|
|
| 图② |
|
|
|
(2)三个正方形A,B,C的面积之间有什么关系?
(3)三个正方形围成的一个直角三角形的三边长之间存在什么关系?
甲乙两座城市的铁路经过技术改造,列车在甲乙两城市间的运行速度从80千米/时提高到100千米/时,运行时间缩短了2.5小时,求甲乙两城市间的铁路路程是多少千米?
如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.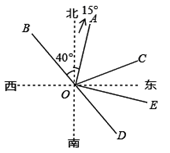
(1)射线OC的方向是___________________;
(2)求∠COD的度数;
(3)若射线OE平分∠COD,求∠AOE的度数.
如图,C、D是线段AB上两点,已知AC:CD:DB=1:2:3,M、N分别为AC、DB的中点,且AB=18cm.
(1)求线段CB的长;
(2)求线段MN的长.
“整体思想”是中学数学解题中一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.如:已知 ,试求多项式
,试求多项式
(1)计算: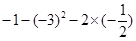 ;
;
(2)解方程: .
.