已知数列 共有
共有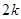 项
项 数列
数列 的前
的前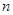 项的和为
项的和为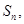 满足
满足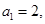
 其中常数
其中常数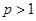
(1)求证:数列 是等比数列;
是等比数列;
(2)若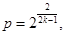 数列
数列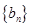 满足
满足 求数列
求数列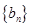 的通项公式
的通项公式
(3)对于(2)中的数列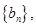 记
记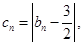 求数列
求数列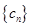 的前
的前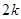 项的和
项的和
如图 是椭圆
是椭圆 的左右顶点
的左右顶点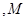 是椭圆上异于
是椭圆上异于 的任意一点
的任意一点 直线
直线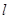 是椭圆的右准线
是椭圆的右准线
(1)若椭圆 的离心率为
的离心率为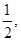 直线
直线 求椭圆
求椭圆 的方程;
的方程;
(2)设直线 交
交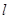 于点
于点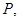 以
以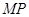 为直径的圆交
为直径的圆交 于
于 若直线
若直线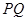 恰好过原点
恰好过原点 求椭圆
求椭圆 的离心率
的离心率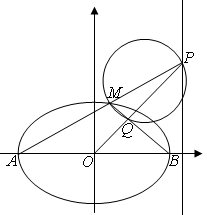
如图 有两条相交直线成
有两条相交直线成 角的直路
角的直路 交点是
交点是 甲、乙两人分别在
甲、乙两人分别在 上,甲的起始位置距离
上,甲的起始位置距离 点
点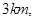 乙的起始位置距离
乙的起始位置距离 点
点 后来甲沿
后来甲沿 的方向
的方向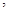 乙沿
乙沿 的方向
的方向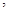 两人同时以
两人同时以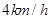 的速度步行
的速度步行
(1)求甲乙在起始位置时两人之间的距离;
(2)设 后甲乙两人的距离为
后甲乙两人的距离为 写出
写出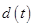 的表达式;当
的表达式;当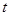 为何值时
为何值时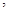 甲乙两人的距离最短
甲乙两人的距离最短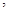 并求出此时两人的最短距离
并求出此时两人的最短距离
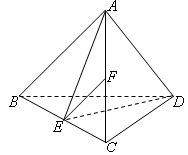
如图 在四面体
在四面体 中
中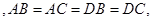 点
点 是
是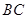 的中点
的中点 点
点 在
在 上,且
上,且


(1)若 平面
平面 求实数
求实数 的值;
的值;
(2)求证:平面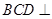 平面
平面
如图 在平面直角坐标系
在平面直角坐标系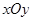 中
中 点
点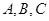 均在单位圆上
均在单位圆上 已知点
已知点 在第一象限的横坐标是
在第一象限的横坐标是 点
点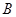 在第二象限
在第二象限 点
点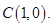
(1)设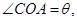 求
求 的值;
的值;
(2)若 为正三角形
为正三角形 求点
求点 的坐标
的坐标