如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.求证: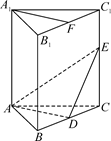
(1)平面ADE⊥平面BCC1B1;
(2)直线A1F∥平面ADE.
已知椭圆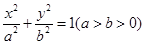 的,离心率为
的,离心率为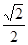 ,
,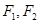 是其焦点,点
是其焦点,点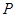 在椭圆上。
在椭圆上。
(Ⅰ)若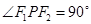 ,且
,且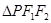 的面积等于
的面积等于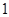 。求椭圆的方程;
。求椭圆的方程;
(Ⅱ)直线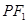 交椭圆于另一点
交椭圆于另一点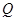 ,分别过点
,分别过点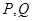 作直线
作直线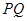 的垂线,交
的垂线,交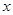 轴于点
轴于点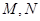 ,当
,当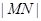 取最小值时,求直线
取最小值时,求直线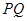 的斜率。
的斜率。
某市现有居民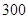 万人,每天有
万人,每天有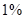 的人选择乘出租车出行,记每个人的乘车里程为
的人选择乘出租车出行,记每个人的乘车里程为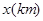 ,
,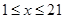 。由调查数据得到
。由调查数据得到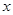 的频率分布直方图(如图)。在直方图的乘车里程分组中,可以用各组的区间中点值代表该组的各个值,乘车里程落人该区间的频率作为乘车里程取区间中点值得概率。现规定乘车里程
的频率分布直方图(如图)。在直方图的乘车里程分组中,可以用各组的区间中点值代表该组的各个值,乘车里程落人该区间的频率作为乘车里程取区间中点值得概率。现规定乘车里程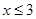 时,乘车费用为
时,乘车费用为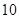 元;当
元;当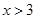 时,每超出
时,每超出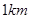 (不足
(不足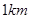 时按
时按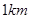 计算),乘车费用增加
计算),乘车费用增加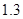 元。
元。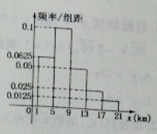
(Ⅰ)试估计乘客的乘车费用不超过15.2元的概率;
(Ⅱ)试估计出租车公司一天的总收入是多小?(精确到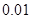 万元)
万元)
如图,在直三棱柱 中,
中,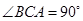 ,
,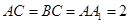 ,
,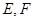 分别是
分别是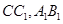 的中点。
的中点。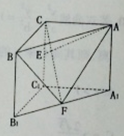
(1)求证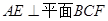 ;
;
(2)求点F到平面ABE的余距离。
在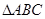 中,角
中,角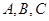 的对边分别是
的对边分别是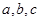 ,且
,且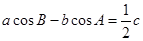 。
。
(1)求证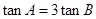 。
。
(2)若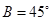 ,
,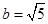 ,求
,求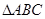 的面积。
的面积。
选修4-5:不等式选讲
设函数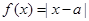 ,
,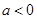
(Ⅰ)证明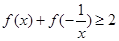
(Ⅱ)若不等式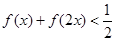 的解2集非空,求
的解2集非空,求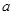 的取值范围。
的取值范围。