某市现有居民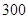 万人,每天有
万人,每天有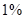 的人选择乘出租车出行,记每个人的乘车里程为
的人选择乘出租车出行,记每个人的乘车里程为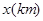 ,
,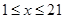 。由调查数据得到
。由调查数据得到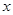 的频率分布直方图(如图)。在直方图的乘车里程分组中,可以用各组的区间中点值代表该组的各个值,乘车里程落人该区间的频率作为乘车里程取区间中点值得概率。现规定乘车里程
的频率分布直方图(如图)。在直方图的乘车里程分组中,可以用各组的区间中点值代表该组的各个值,乘车里程落人该区间的频率作为乘车里程取区间中点值得概率。现规定乘车里程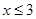 时,乘车费用为
时,乘车费用为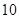 元;当
元;当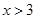 时,每超出
时,每超出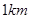 (不足
(不足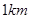 时按
时按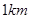 计算),乘车费用增加
计算),乘车费用增加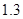 元。
元。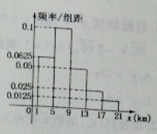
(Ⅰ)试估计乘客的乘车费用不超过15.2元的概率;
(Ⅱ)试估计出租车公司一天的总收入是多小?(精确到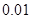 万元)
万元)
(本题满分14分)已知函数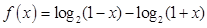 .
.
(1)求函数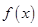 的定义域;
的定义域;
(2)判断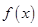 的奇偶性;
的奇偶性;
(3)方程 是否有根?如果有根
是否有根?如果有根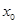 ,请求出一个长度为
,请求出一个长度为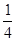 的区间
的区间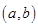 ,使
,使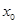
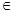
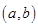 ;如果没有,请说明理由?(注:区间的长度为
;如果没有,请说明理由?(注:区间的长度为 ).
).
.已知圆C: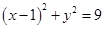 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线
l交圆C于A、B两点.
(1)当l经过圆心C时,求直线l的方程;
(2)当弦AB被点P平分时,写出直线l的方程;
(3) 当直线l的倾斜角为45º时,求弦AB的长.
(本小题满分12分)如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证:
(1) FD∥平面ABC;
(2)AF⊥平面EDB.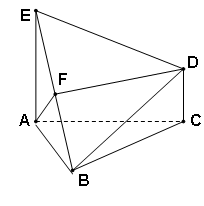
(本题满分12分)某公司试销一种成本单价为500元/件的新产品,规定试销时销售
单价不低于成本单价,又不高于800元/件,经试销调查,发现销售量y(件)与销售单价 (元
(元
/件),可近似看做一次函数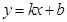 的关系(如下图所示).
的关系(如下图所示).
(1)根据图象,求一次函数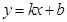 的表达式;
的表达式;
(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元, ①求S关于 的函数
的函数
表达式;②求该公司可获得的最大毛利润,并求出相应的销售单价.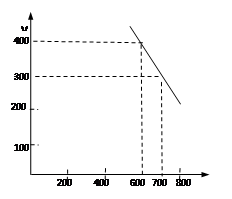
(本题满分12分)求圆心在直线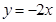 上,并且与直线
上,并且与直线 相切于点
相切于点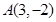
的圆的方程。