(本题满分18分,第1小题4分,第2小题6分,第3小题8分)
已知数列{an}满足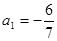 ,
,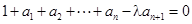 (其中λ≠0且λ≠–1,n∈N*),
(其中λ≠0且λ≠–1,n∈N*), 为数列{an}的前
为数列{an}的前 项和.
项和.
(1) 若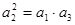 ,求
,求 的值;
的值;
(2) 求数列{an}的通项公式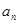 ;
;
(3) 当 时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
已知直线是过点 ,方向向量为
,方向向量为 的直线,圆方程
的直线,圆方程
(1)求直线的参数方程
(2)设直线与圆相交于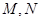 两点,求
两点,求 的值
的值
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连结EC、CD.
(Ⅰ)求证:直线AB是⊙O的切线;
(Ⅱ)若tan∠CED= ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
已知函数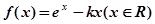
(1)若 ,试确定函数
,试确定函数 的单调区间;
的单调区间;
(2)若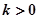 且对任意
且对任意 ,
, 恒成立,试确定实数
恒成立,试确定实数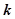 的取值范围;
的取值范围;
(3)设函数 ,求证:
,求证: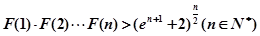
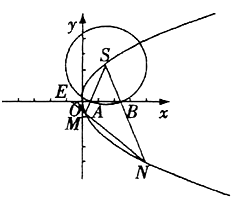
已知点F是抛物线C: 的焦点,S是抛物线C在第一象限内的点,且|SF|=
的焦点,S是抛物线C在第一象限内的点,且|SF|= .
.
(Ⅰ)求点S的坐标;
(Ⅱ)以S为圆心的动圆与 轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;
轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;
①判断直线MN的斜率是否为定值,并说明理由;
②延长NM交 轴于点E,若|EM|=
轴于点E,若|EM|= |NE|,求cos∠MSN的值.
|NE|,求cos∠MSN的值.
如图:四边形 是梯形,
是梯形, ,
,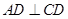 ,三角形
,三角形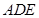 是等边三角形,且平面
是等边三角形,且平面
 平面
平面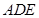 ,
, ,
, ,
,

(1)求证: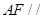 平面
平面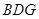 ;
;
(2)求二面角 的余弦值.
的余弦值.