已知曲线 :
: (
( 为参数),
为参数),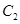 :
: (
( 为参数).
为参数).
(1)化 ,
,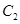 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若 上的点
上的点 对应的参数为
对应的参数为 ,
, 为
为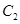 上的动点,求
上的动点,求 中点
中点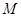 到直线
到直线 (
( 为参数)距离的最小值.
为参数)距离的最小值.
已知 ,
, ,且
,且 //
//  .设函数
.设函数 .
.
(Ⅰ)求函数 的解析式.
的解析式.
(Ⅱ)若在锐角 中,
中, ,边
,边 ,求
,求 周长的最大值.
周长的最大值.
设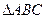 的内角A、B、C所对的边分别为a、b、c,已知
的内角A、B、C所对的边分别为a、b、c,已知
(I)  求
求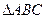 的第三条边长c;
的第三条边长c;
(II)求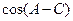 的值。
的值。
已知等差数列{an}满足a2=0,a6+a8= -10
(I)求数列{an}的通项公式;
(II)求数列{ }的前n项和。
}的前n项和。
如图在长方形ABCD中,已知AB=4,BC=2 ,M,N,P为长方形边上的中点,Q是边CD上的点,且CQ=3DQ,求 的值.
的值.
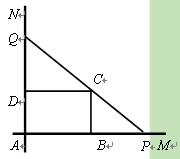
如图,互相垂 直的两条公路
直的两条公路 、
、 旁有一矩形花园
旁有一矩形花园 ,现欲将其扩建成一个
,现欲将其扩建成一个 更大的三角形花园
更大的三角形花园 ,要求
,要求 在射线
在射线 上,
上, 在射线
在射线 上,且
上,且 过点
过点 ,其中
,其中 米,
米,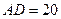 米. 记三角形花园
米. 记三角形花园 的面积为
的面积为 .
.
(1)设

 米,将
米,将 表示成
表示成 的函数.
的函数.
(2) 当
当 的长度是多少时,
的长度是多少时, 最小?并求
最小?并求 的最小值.
的最小值.
(3)要使 不小于
不小于 平方米,则
平方米,则 的长应在什么范围内?
的长应在什么范围内?