某运输公司有12名驾驶员和19名工人，有8辆载重量为10吨的甲型卡车和7辆载重量为6吨的乙型卡车．某天需运往
地至少72吨的货物，派用的每辆车须满载且只运送一次．派用的每吨甲型卡车须配2名工人，运送一次可得利润450元；派用的每辆乙型卡车须配1名工人，运送一次可得利润350元．问该公司如何派用两类卡车的车辆数可得最大利润？
函数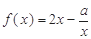
的定义域为(0，1]（
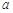为实数）．
⑴当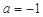
时，求函数
的值域；
⑵若函数在定义域上是减函数，求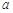的取值范围；
为了解某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：
| 喜爱打篮球 |
不喜爱打篮球 |
合计 |
|
| 男生 |
5 |
||
| 女生 |
10 |
||
| 合计 |
５０ |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为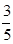
．
（1）请将上面的列联表补充完整；
（2）是否有99．5％的把握认为喜爱打篮球与性别有关？说明你的理由；
（3）已知喜爱打篮球的10位女生中，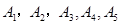
还喜欢打羽毛球，
还
喜欢打乒乓球，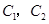
还喜欢踢足球，现再从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的女生中各选出1名进行其他方面的调查，求
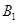和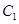
不全被选中的概率．
袋中装有m个红球和n个白球，m≥n≥2，这些红球和白球除了颜色不同以外，其余都相同．从袋中同时取出2个球．
（1）若取出是2个红球的概率等于取出的是一红一白的2个球的概率的整数倍，试证：m 必为奇数；
（2）若取出的球是同色的概率等于不同色的概率，试求m+n≤40的所有数组(m，n)．
在长度为10cm的线段AD上任取两点B、C，在B、C处折断此线段而得一折线，求此折线能构成三角形的概率．
有9名学生，其中2名会下象棋但不会下围棋，3名会下围棋但不会下象棋，4名既会下围棋又会下象棋；现在要从这9名学生中选出2名学生，一名参加象棋比赛，另一名参加围棋比赛，共有多少种不同的选派方法？