为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品,已知该单位每月的处理量最少400吨,最多600吨,月处理成本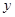 (元)与月处理量
(元)与月处理量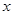 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为:
且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
|
如图,直四棱柱ABCD—A1B1C1D1的高为3,底面是边长为4且∠DAB = 60°的菱形,AC BD = O,A1C1
BD = O,A1C1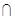 B1D1 = O1,E是O1A的中点.
B1D1 = O1,E是O1A的中点.
已知函数 .
.
(1)若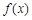 在x = 0处取得极值为 – 2,求a、b的值;
在x = 0处取得极值为 – 2,求a、b的值;
(2)若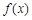 在
在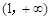 上是增函数,求实数a的取值范围.
上是增函数,求实数a的取值范围.
设集合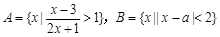 ,若
,若 ,求实数a的取值范围.
,求实数a的取值范围.
已知函数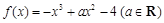 .
.
(1)若函数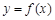 的图象在点P(1,
的图象在点P(1,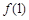 )处的切线的倾斜角为
)处的切线的倾斜角为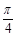 ,求实数a的值;
,求实数a的值;
(2)设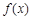 的导函数是
的导函数是 ,在 (1) 的条件下,若
,在 (1) 的条件下,若 ,求
,求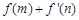 的最小值.
的最小值.
(3)若存在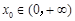 ,使
,使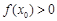 ,求a的取值范围.
,求a的取值范围.
某工厂在试验阶段大量生产一种零件.这种零件有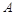 、
、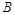 两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为
两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为 ,至少一项技术指标达标的概率为
,至少一项技术指标达标的概率为 .按质量检验规定:两项技术指标都达标的零件为合格品.
.按质量检验规定:两项技术指标都达标的零件为合格品.
(1)求一个零件经过检测为合格品的概率是多少?
(2)任意依次抽出5个零件进行检测,求其中至多3个零件是合格品的概率是多少?