已知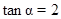 ,
,
求(Ⅰ) 的值;(Ⅱ)
的值;(Ⅱ)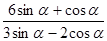 的值.
的值.
某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如下图所示.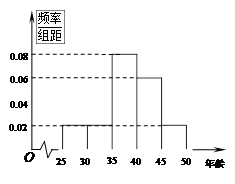
(Ⅰ)下表是年龄的频数分布表,求正整数a,b的值;
| 区间 |
[25,30) |
[30,35) |
[35,40) |
[40,45) |
[45,50] |
| 人数 |
50 |
50 |
 |
150 |
 |
(Ⅱ) 现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(III)在(Ⅱ)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB, PC的中点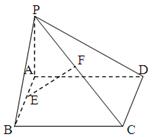
(1)求证:EF∥平面PAD;
(2)求证:EF⊥CD;
(3)若ÐPDA=45°,求EF与平面ABCD所成的角的大小.
某设备的使用年限 与所支出的总费用
与所支出的总费用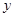 (万元)有如下的统计资料:
(万元)有如下的统计资料:
使用年限 |
1 |
2 |
3 |
4 |
总费用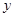 |
1.5 |
2 |
3 |
3.5 |
(Ⅰ)在给定的坐标系中画出表中数据的散点图;
(Ⅱ)求出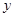 关于
关于 的线性回归方程
的线性回归方程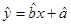 ;
;
(III)当使用10年时,所支出的总费用约为多少万元。
参考公式:回归方程为 其中
其中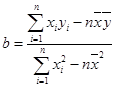 ,
, 
以下茎叶图记录了甲、乙两组各四名同学的植树棵树。乙组记录中有一个数据模糊,无法确认,在图中以X表示.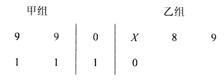
(1)求甲组同学植树棵树的平均数和方差;(参考公式: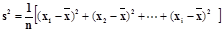 )
)
(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.