某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.,当每辆车的月租金定为x元时,租赁公司的月收益为y元,
(1)试写出x,y的函数关系式(不要求写出定义域);
(2)租赁公司某月租出了88辆车,求租赁公司的月收益多少元?
已知函数
(1)求不等式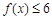 的解集;
的解集;
(2)若关于x的不等式 的解集非空,求实数
的解集非空,求实数 的取值范围.
的取值范围.
选修4-4:坐标系与参数方程已知直线l: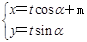 (t为参数)恒经过椭圆C:
(t为参数)恒经过椭圆C: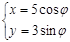 (j为参数)的右焦点F.
(j为参数)的右焦点F.
(Ⅰ)求m的值;
(Ⅱ)设直线l与椭圆C交于A,B两点,求|FA|·|FB|的最大值与最小值.
选修4-1:几何证明选讲如图,已知圆上的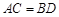 ,过C点的圆的切线与BA的延长线交于E点.
,过C点的圆的切线与BA的延长线交于E点.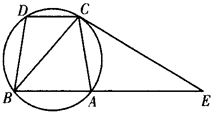
(Ⅰ)求证:∠ACE=∠BCD;
(Ⅱ)若BE=9,CD=1,求BC的长.
已知函数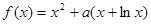 ,
,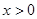 ,
, 是常数.
是常数.
(1)求函数 的图象在点
的图象在点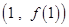 处的切线方程;
处的切线方程;
(2)若函数 图象上的点都在第一象限,试求常数
图象上的点都在第一象限,试求常数 的取值范围;
的取值范围;
(3)证明: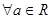 ,存在
,存在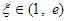 ,使
,使 .
.
如图,在斜三棱柱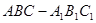 中,
中,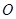 是
是 的中点,
的中点, ⊥平面
⊥平面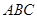 ,
, ,
,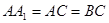 .
.
(Ⅰ)求证: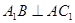 ;
;
(Ⅱ)求二面角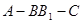 的余弦值.
的余弦值.