已知向量 , 设函数
, 设函数 .
.
(1)求 的单调递增区间;
的单调递增区间;
(2)求 在
在 上的最大值和最小值.
上的最大值和最小值.
(本小题满分13分)从甲、乙两班某项测试成绩中各随机抽取5名同学的成绩,得到如下茎叶图.已知甲班样本成绩的中位数为13, 乙班样本成绩的平均数为16.
(1)求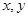 的值;
的值;
(2)试估计甲、乙两班在该项测试中整体水平的高低(只需写出结论);
(3)从两组样本成绩中分别去掉一个最低分和一个最高分,再从两组
剩余成绩中分别随机选取一个成绩,求这两个成绩的和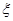 的分布列及数学期望.
的分布列及数学期望.
(注:方差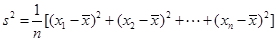 ,其中
,其中 为
为 ,
,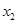 , ,
, , 的平均数.)
的平均数.)
(本小题满分13分)已知函数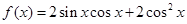 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)当 时,求函数
时,求函数 的最大值及取得最大值时的
的最大值及取得最大值时的 值.
值.
(本小题12分)已知二次函数 满足
满足 且
且 .(1)求
.(1)求 的解析式; (2) 当
的解析式; (2) 当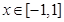 时,不等式:
时,不等式: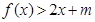 恒成立,求实数
恒成立,求实数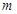 的范围.(3)设
的范围.(3)设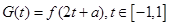
 ,求
,求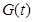 的最大值;
的最大值;
(满分12分)已知 对一切实数
对一切实数 都有
都有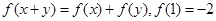 ,当
,当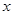 >0时,
>0时, <0.
<0.
(1)证明 为
为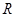 上的减函数;(2)解不等式
上的减函数;(2)解不等式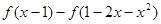 <4
<4
(本小题12分)判断函数
在区间 上的单调性,并用函数单调性的定义加以证明.
上的单调性,并用函数单调性的定义加以证明.