
(1)若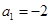 ,点
,点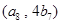 在函数
在函数 的图像上,求数列
的图像上,求数列 的前
的前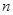 项和
项和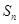 ;
;
(2)若a1=1,函数f(x)的图像在点(a2,b2)处的切线在x轴上的截距为2- ,求数列
,求数列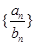 的前n项和Tn.
的前n项和Tn.
(本小题12分)已知函数
 。
。
(1)当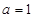 时,判断
时,判断 的单调性;
的单调性;
(2)若 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数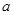 的取值范围;
的取值范围;
(本小题12分) 如图,在五面体 中,
中, ∥
∥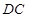 ,
,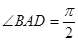 ,
, ,四边形
,四边形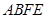 为平行四边形,
为平行四边形,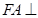 平面
平面 ,
,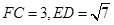 .
.
求:(1)直线 到平面
到平面 的距离;
的距离;
(2)二面角 的平面角的正切值.
的平面角的正切值.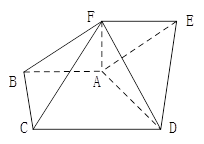
(本小题12分)已知三次函数 的导函数
的导函数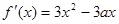 ,
, ,(
,( ,
,
 ).
).
(1)若曲线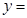
 在点(
在点(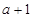 ,
, )处切线的斜率为12,求
)处切线的斜率为12,求 的值;
的值;
(2)若 在区间[-1,1]上的最小值,最大值分别为-2和1,且
在区间[-1,1]上的最小值,最大值分别为-2和1,且 ,求函数
,求函数 的解析式.
的解析式.
(本小题10分)如图,四棱锥 的底面是正方形,
的底面是正方形, ,点E在棱PB上.
,点E在棱PB上.
(1)求证:平面 ;
;
(2)当 且E为PB的中点时,求AE与平面PDB所成的角的大小.
且E为PB的中点时,求AE与平面PDB所成的角的大小.
(本小题满分12分)
数列 满足
满足
(1)设 ,求证
,求证 是等比数列;(2) 求数列
是等比数列;(2) 求数列 的通项公式;
的通项公式;
(3)设 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证: