(本小题10分)如图,四棱锥 的底面是正方形,
的底面是正方形, ,点E在棱PB上.
,点E在棱PB上.
(1)求证:平面 ;
;
(2)当 且E为PB的中点时, 求AE与平面PDB所成的角的大小.
且E为PB的中点时, 求AE与平面PDB所成的角的大小.
已知等差数列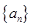 的首项为
的首项为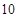 ,公差为
,公差为 ,等比数列
,等比数列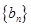 的首项为
的首项为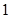 ,公比为
,公比为 ,
,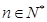 .
.
(1)求数列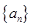 与
与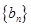 的通项公式;
的通项公式;
(2)设第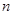 个正方形的边长为
个正方形的边长为 ,求前
,求前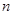 个正方形的面积之和
个正方形的面积之和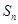 .
.
(注: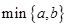 表示
表示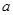 与
与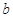 的最小值.)
的最小值.)
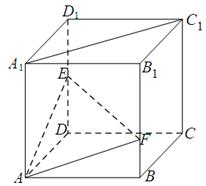
如图,在棱长为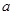 的正方体
的正方体 中,点
中,点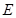 是棱
是棱 的中点,点
的中点,点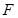 在棱
在棱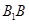 上,且满足
上,且满足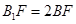 .
.
(1)求证: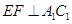 ;
;
(2)在棱 上确定一点
上确定一点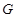 ,使
,使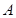 、
、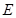 、
、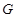 、
、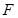 四点共面,并求此时
四点共面,并求此时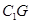 的长;
的长;
(3)求平面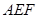 与平面
与平面 所成二面角的余弦值.
所成二面角的余弦值.
甲、乙、丙三人参加某次招聘会,假设甲能被聘用的概率是 ,甲、丙两人同时不能被聘用的概率是
,甲、丙两人同时不能被聘用的概率是 ,乙、丙两人同时能被聘用的概率为
,乙、丙两人同时能被聘用的概率为 ,且三人各自能否被聘用相互独立.
,且三人各自能否被聘用相互独立.
(1)求乙、丙两人各自被聘用的概率;
(2)设 为甲、乙、丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值,求
为甲、乙、丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值,求 的分布列与均值(数学期望).
的分布列与均值(数学期望).
已知函数 的图象经过点
的图象经过点 .
.
(1)求实数 的值;
的值;
(2)设 ,求函数
,求函数 的最小正周期与单调递增区间.
的最小正周期与单调递增区间.
设函数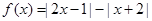
(1)求不等式 的解集;
的解集;
(2)若关于 的不等式
的不等式 在
在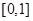 上无解,求实数
上无解,求实数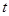 的取值范围
的取值范围