在平面直角坐标系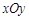 中,已知圆
中,已知圆 ,
,
圆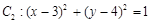 .
.
(Ⅰ)若过点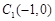 的直线
的直线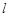 被圆
被圆 截得的弦长为
截得的弦长为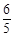 ,求直线
,求直线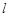 的方程;
的方程;
(Ⅱ)圆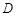 是以1为半径,圆心在圆
是以1为半径,圆心在圆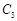 :
: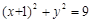 上移动的动圆 ,若圆
上移动的动圆 ,若圆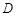 上任意一点
上任意一点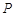 分别作圆
分别作圆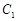 的两条切线
的两条切线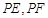 ,切点为
,切点为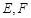 ,求
,求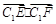 的取值范围 ;
的取值范围 ;
(Ⅲ)若动圆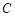 同时平分圆
同时平分圆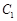 的周长、圆
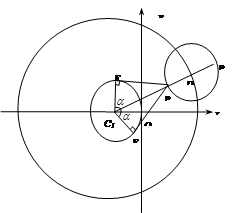
的周长、圆 的周长,如图所示,则动圆
的周长,如图所示,则动圆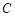 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
如图,圆柱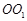 内有一个三棱柱
内有一个三棱柱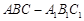 ,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径.
,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径.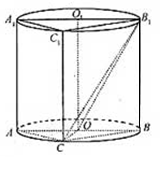
(Ⅰ)证明:平面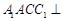 平面
平面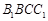 ;
;
(Ⅱ)设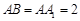 ,在圆柱
,在圆柱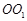 内随机选取一点,记该点取自于三棱柱
内随机选取一点,记该点取自于三棱柱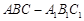 内的概率为
内的概率为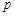 .
.
(ⅰ)当点C在圆周上运动时,求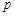 的最大值;
的最大值;
(ii)记平面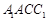 与平面
与平面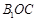 所成的角为
所成的角为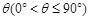 ,当
,当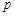 取最大值时,求
取最大值时,求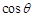 的值.
的值.
(本小题共12分)近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
| “厨余垃圾”箱 |
“可回收物”箱 |
“其他垃圾”箱 |
|
| 厨余垃圾 |
400 |
100 |
100 |
| 可回收物 |
30 |
240 |
30 |
| 其他垃圾 |
20 |
20 |
60 |
(Ⅰ)试估计厨余垃圾投放正确的概率;
(Ⅱ)试估计生活垃圾投放错误的概率;
(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为 ,其中
,其中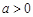 ,
,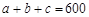 。当数据
。当数据 的方差
的方差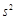 最大时,写出
最大时,写出 的值(结论不要求证明),并求此时
的值(结论不要求证明),并求此时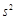 的值.
的值.
(注: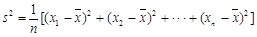 ,其中
,其中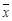 为数据
为数据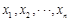 的平均数)
的平均数)
号码为1、2、3、4、5、6的六个大小相同的球,放入编号为1、2、3、4、5、6的六个盒子中,每个盒子只能放一个球.
(Ⅰ)若1号球只能放在1号盒子中,2号球只能放在2号的盒子中,则不同的放法有多少种?
(Ⅱ)若3号球只能放在1号或2号盒子中,4号球不能放在4号盒子中,则不同的放法有多少种?
(Ⅲ)若5、6号球只能放入号码是相邻数字的两个盒子中,则不同的放法有多少种?
某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段:  ,
, ,…,
,…, 后得到如下频率分布直方图.
后得到如下频率分布直方图.
(Ⅰ)求分数在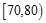 内的频率;
内的频率;
(Ⅱ)用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任意选取2人,求其中恰有1人的分数不低于90分的概率.