(本题满分14分)
如图,圆锥的顶点是S,底面中心为O.OC是与底面直径AB垂直的一条半径,D是母线SC的中点.
(1)求证:BC与SA不可能垂直.
(2)设圆锥的高为4,异面直线AD与BC所成角的余弦值为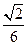 ,求圆锥的体积.
,求圆锥的体积.
(本题满分12分)已知A(2,0),B(0,2),C(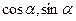 ),且0<
),且0< <
<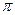 .
.
(1)若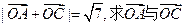 的夹角;
的夹角;
(2)若 的值.
的值.
已知函数 满足
满足 ,
, 是不为
是不为 的实常数。
的实常数。
(1)若当 时,
时, ,求函数
,求函数 的值域;
的值域;
(2)在(1)的条件下,求函数 的解析式;
的解析式;
(3)若当 时,
时, ,试研究函数
,试研究函数 在区间
在区间 上是否可能是单调函数?
上是否可能是单调函数?
若可能,求出 的取值范围;若不可能,请说明理由。
的取值范围;若不可能,请说明理由。
已知函数 满足
满足 ,
, 是不为
是不为 的实常数。
的实常数。
(1)若函数 是周期函数,写出符合条件
是周期函数,写出符合条件 的值;
的值;
(2)若当 时,
时, ,且函数
,且函数 在区间
在区间 上的值域是闭区间,求
上的值域是闭区间,求 的取值范围;
的取值范围;
(3)若当 时,
时, ,试研究函数
,试研究函数 在区间
在区间 上是否可能是单调函数?若可能,求出
上是否可能是单调函数?若可能,求出 的取值范围;若不可能,请说明理由。
的取值范围;若不可能,请说明理由。
已知函数 是奇函数。
是奇函数。
(1)求 的值;
的值;
(2)请讨论它的单调性,并给予证明。