如图（1）是一辆汽车速度随时间而变化的情况示意图．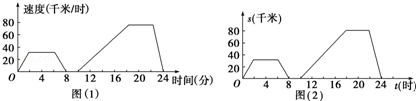
（1）汽车从出发到最后停止共经过多少时间？它的最高时速是多少？
（2）汽车在哪些时间段保持匀速行驶？时速分别是多少？
（3）出发后8分到10分之间可能发生了什么情况？
（4）如果纵轴表示路程s（千米）．如图（2），横轴表示时间t（时）．这是一个骑自行车者离家距离与时间的关系图象．在出发后8小时到10小时之间可能发生了什么情况？骑自行车者在哪些时间段保持匀速运动？速度分别是多少？
（本小题满分14分）如图，半径为r的圆M与正三角形ABC的两边AB,AC相切，且与圆弧BEC相切.圆M与OA相交于E,N两点.已知圆弧BEC所在圆半径为R，圆心为O.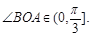 
（1）求
的最大值；
（2）若
求DN的最大值.
（本小题满分14分）如图四棱锥P-ABCD中，底面ABCD是菱形，∠BAD＝60°，AD＝1，侧面PAD是正三角形，且与底面ABCD垂直，Q是AD的中点．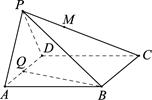
（1）求四棱锥P-ABCD的体积；
（2）M在线段PC上，PM＝tPC，问线段BC上是否存在一点R，使得当t∈(0，1)时，总有BQ∥平面MDR？若存在，确定R点位置；若不存在，请说明理由．
（本小题满分14分）在平面直角坐标系
中，角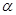
的终边经过点
．
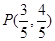（1）求
的值；
（2）若
关于
轴的对称点为
，求
的值．
（本小题满分14分）已知椭圆
的一个焦点与抛物线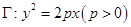
的焦点重合，椭圆的离心率为
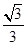且过点
．
（Ⅰ）求椭圆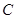
和抛物线
的标准方程；
（Ⅱ）设直线
过椭圆的右焦点
且与椭圆交于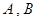
两点，在椭圆上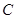是否存在点
，使得当绕转到某一位置时，有
成立？若存在，求出所有的的坐标与的方程；若不存在，说明理由．
（本小题满分14分）已知函数
．
（Ⅰ）若
，且函数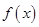
在定义域内单调递增，求实数
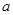的取值范围；
（Ⅱ）若
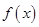，且函数在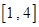
上恰有两个零点，求实数
的取值范围．