(本小题满分14分)如图四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AD=1,侧面PAD是正三角形,且与底面ABCD垂直,Q是AD的中点.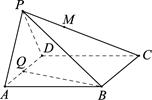
(1)求四棱锥P-ABCD的体积;
(2)M在线段PC上,PM=tPC,问线段BC上是否存在一点R,使得当t∈(0,1)时,总有BQ∥平面MDR?若存在,确定R点位置;若不存在,请说明理由.
口袋中有质地、大小完全相同的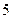 个球,编号分别为
个球,编号分别为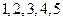 ,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.
,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.
(1)求甲赢且编号的和为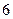 的事件发生的概率;
的事件发生的概率;
(2)这种游戏规则公平吗?试说明理由.
某商场有奖销售中,购满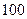 元商品得
元商品得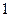 张奖券,多购多得。
张奖券,多购多得。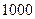 张奖券为一个开奖单位,设特等奖
张奖券为一个开奖单位,设特等奖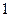 个,一等奖
个,一等奖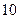 个,二等奖
个,二等奖 个。设
个。设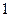 张奖券中特等奖、一等奖、二等奖的事件分别为
张奖券中特等奖、一等奖、二等奖的事件分别为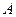 、
、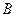 、
、 ,求:
,求:
(1)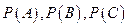 ;
;
(2)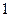 张奖券的中奖概率;
张奖券的中奖概率;
(3)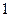 张奖券不中特等奖且不中一等奖的概率。
张奖券不中特等奖且不中一等奖的概率。
如图,一面旗帜由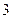 部分构成,这
部分构成,这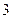 部分必须分别着上不同的颜色,现有红、黄、蓝、黑四种颜色可供选择,利用树状图列出所有可能结果,并计算下列事件的概率:
部分必须分别着上不同的颜色,现有红、黄、蓝、黑四种颜色可供选择,利用树状图列出所有可能结果,并计算下列事件的概率:
(1)红色不被选中;
(2)第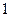 部分是黑色并且第
部分是黑色并且第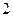 部分是红色.
部分是红色.
对一批衬衣进行抽检,结果如下表:
(1)完成上面统计表;
(2)事件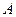 为任取一件衬衣为次品,求
为任取一件衬衣为次品,求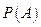 ;
;
(3)为了保证买到次品的顾客能够及时更换,销售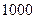 件衬衣,至少需要进货多少件衬衣?
件衬衣,至少需要进货多少件衬衣?
给定整数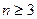 ,证明:存在n个互不相同的正整数组成的集合S,使得对S的任意两个不同的非空子集A,B,数
,证明:存在n个互不相同的正整数组成的集合S,使得对S的任意两个不同的非空子集A,B,数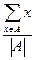 与
与
是互素的合数.(这里 与
与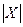 分别表示有限数集
分别表示有限数集 的所有元素之和及元素个数.)
的所有元素之和及元素个数.)