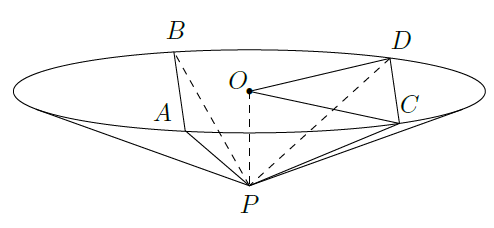
如图，圆锥顶点为P.底面圆心为O，其母线与底面所成的角为22-优题课

题文

如图，圆锥顶点为 $P$ .底面圆心为 $O$ ，其母线与底面所成的角为 $22 . 5^{°}$ . $A B$ 和 $C D$ 是底面圆 $O$ 上的两条平行的弦，轴 $O P$ 与平面 $P C D$ 所成的角为 $60^{°}$ ，

（Ⅰ）证明：平面 $P A B$ 与平面 $P C D$ 的交线平行于底面；
（Ⅱ）求 $\cos ∠ C O D$ .

科目数学题型解答题难度较易

登录免费查看答案和解析

相关试题

已知二次函数y＝f(x)(x∈R)的图像是一条开口向下且对称轴为x＝3的抛物线，试比较大小：
(1)f(6)与f(4)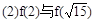

已知集合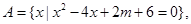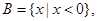若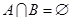，则实数m的取值范围是（）

记关于x的不等式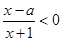的解集为P，不等式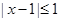的解集为Q.
（1）若a=3,求P
（2）若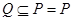求正数a的取值范围

已知集合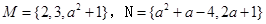且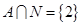，求a的值。

如图,已知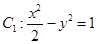曲线,曲线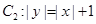,P是平面上一点,若存在过点P的直线与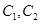都有公共点,则称P为“C₁—C₂型点”.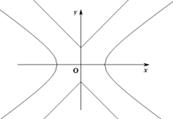

(1)在正确证明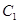的左焦点是“C₁—C₂型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线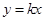与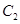有公共点,求证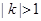,进而证明原点不是“C₁—C₂型点”;
(3)求证:圆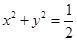内的点都不是“C₁—C₂型点”.

试卷网试题网古诗词网作文网范文网