山东鲁洁棉业公司的科研人员在7块并排、形状大小相同的试验田上对某棉花新品种进行施化肥量x对产量y影响的试验,得到如下表所示的一组数据(单位:kg).
| 施化肥量x |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
| 棉花产量y |
330 |
345 |
365 |
405 |
445 |
450 |
455 |
(1)画出散点图;
(2)判断是否具有相关关系.
如图,在四棱锥E-ABCD中,底面ABCD为正方形, AE⊥平面CDE,已知AE=3,DE=4.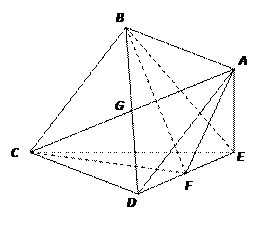
(Ⅰ)若F为DE的中点,求证:BE//平面ACF;
(Ⅱ)求直线BE与平面ABCD所成角的正弦值
已知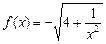 ,点
,点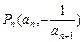 在曲线
在曲线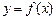 上
上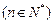 且
且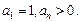 (Ⅰ)求证:数列
(Ⅰ)求证:数列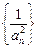 为等差数列,并求数列
为等差数列,并求数列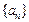 的通项公式;
的通项公式;
(Ⅱ)设数列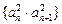 的前n项和为
的前n项和为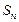 ,若对于任意的
,若对于任意的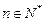 ,存在正整数t,使得
,存在正整数t,使得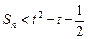 恒成立,求最小正整数t的值
恒成立,求最小正整数t的值
设递增等差数列 的前
的前 项和为
项和为 ,已知
,已知 ,
, 是
是 和
和 的等比中项,
的等比中项,
(I)求数列 的通项公式
的通项公式
(II )求数列
)求数列 的前
的前 项和
项和
(本题满分16分)设函数y=f(x)对任意实数x,都有f(x)=2f(x+1),当x∈[0,1]时,f(x)= x2(1-x).
x2(1-x).
(Ⅰ)已知n∈N+,当x∈[n,n+1]时,求y=f(x)的解析式;
(Ⅱ)求证:对于任意的n∈N+,当x∈[n,n+1]时,都有|f(x)|≤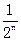 ;
;
(Ⅲ)对于函数y=f(x) (x∈[0,+∞
(x∈[0,+∞ ,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由
,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由
(本题满分16分)(Ⅰ)试比较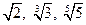 的大小;
的大小;
(Ⅱ)试比较nn+1与(n+1)n(n∈N+)的大小,根据(Ⅰ)的结果猜测一个一般性结论,并加以证明.