某城区为研究城镇居民月家庭人均生活费支出和月人均收入的相关关系,随机抽取10户进行调查,其结果如下:
| 月人均收入x(元) |
300 |
390 |
420 |
504 |
570 |
700 |
746 |
800 |
850 |
1080 |
| 月人均生活费y(元) |
255 |
324 |
330 |
345 |
450 |
520 |
580 |
650 |
700 |
750 |
利用上述资料:
(1)画出散点图;
(2)如果变量x与y之间具有线性相关关系,求出回归直线方程;
(3)测算人均收入为280元时,人均生活费支出应为多少元?
如图,在平面直角坐标系 中,点A(0,3),直线
中,点A(0,3),直线 :
: ,设圆
,设圆 的半径为1,圆心在
的半径为1,圆心在 上.
上.
(1)若圆心 也在直线
也在直线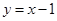 上,过点A作圆
上,过点A作圆 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆 上存在点
上存在点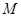 ,使
,使 ,求圆心
,求圆心 的横坐标
的横坐标 的取值范围.
的取值范围.
正项数列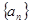 满足:
满足: .
.
(1)求数列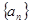 的通项公式
的通项公式 ;
;
(2)令 ,求数列
,求数列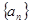 的前
的前 项和
项和 .
.
已知函数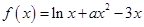 ,且在
,且在 时函数取得极值.
时函数取得极值.
(1)求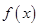 的单调增区间;
的单调增区间;
(2)若 ,
,
(Ⅰ)证明:当 时,
时,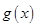 的图象恒在
的图象恒在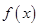 的上方;
的上方;
(Ⅱ)证明不等式 恒成立.
恒成立.
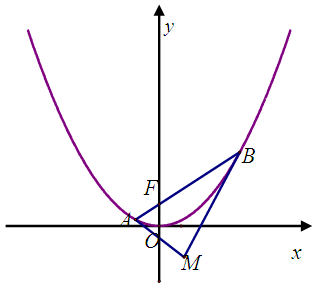
如图示:已知抛物线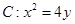 的焦点为
的焦点为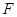 ,过点
,过点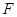 作直线
作直线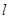 交抛物线
交抛物线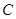 于
于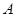 、
、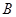 两点,经过
两点,经过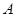 、
、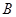 两点分别作抛物线
两点分别作抛物线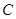 的切线
的切线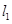 、
、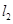 ,切线
,切线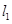 与
与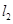 相交于点
相交于点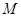 .
.
(1)当点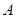 在第二象限,且到准线距离为
在第二象限,且到准线距离为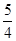 时,求
时,求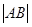 ;
;
(2)证明: .
.
椭圆以坐标轴为对称轴,且经过点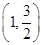 、
、 .记其上顶点为
.记其上顶点为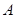 ,右顶点为
,右顶点为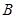 .
.
(1)求圆心在线段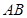 上,且与坐标轴相切于椭圆焦点的圆的方程;
上,且与坐标轴相切于椭圆焦点的圆的方程;
(2)在椭圆位于第一象限的弧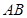 上求一点
上求一点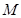 ,使
,使 的面积最大.
的面积最大.