如图，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA边上的中点，阅读下列材料，
（1）连接AC、BD，由三角形中位线的性质定理可证四边形EFGH是________；
（2）对角线AC、BD满足条件_______时，四边形EFGH是矩形；
（3）对角线AC、BD满足条件_______时，四边形EFGH是菱形；
（4）对角线AC、BD满足条件_________时，四边形EFGH是正方形．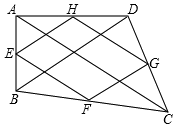
如图1所示，已知直线
与x轴、y轴分别交于A、C两点，抛物线
经过A、C两点，点B是抛物线与x轴的另一个交点，当
时，y取最大值
.
（1）求抛物线和直线的解析式；
（2）设点P是直线AC上一点，且
，求点P的坐标；
（3）若直线
与（1）中所求的抛物线交于M、N两点，问:
①是否存在a的值，使得∠MON=900？若存在，求出a的值；若不存在，请说明理由；
②猜想当∠MON＞900时，a的取值范围（不写过程，直接写结论）.
（参考公式：在平面直角坐标系中，若M（x1，y1），N（x2，y2），则M，N两点间的距离为
）
如图1，点C将线段AB分成两部分，如果
，那么称点C为线段AB的黄金分割点。某数学兴趣小组在进行课题研究时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1、S2，如果
，那么称直线l为该图形的黄金分割线.
（1）如图2，在△ABC中，∠A=360°，AB=AC，∠C的平分线交AB于点D，请问点D是否是AB边上的黄金分割点，并证明你的结论；
（2）若△ABC在（1）的条件下，如图（3），请问直线CD是不是△ABC的黄金分割线，并证明你的结论；
（3）如图4，在直角梯形ABCD中，∠D=∠C=900，对角线AC、BD交于点F，延长AB、DC交于点E，连接EF交梯形上、下底于G、H两点，请问直线GH是不是直角梯形ABCD的黄金分割线，并证明你的结论.
一辆客车从甲地开往乙地，一辆出租车从乙地开往甲地，两车同时出发，设客车离甲
地的距离为y1千米，出租车离甲地的距离为y2千米，两车行驶的时间为x小时，y1、y2关于x的函数图像如下图
所示：
（1）根据图像，直接写出y1、y2关于x的函数关系式；
（2）若两车之间的距离为S千米，请写出S关于x的函数关系式；
（3）甲、乙两地间有A、B两个加油站，相距200千米，若客车进入A加油站时，出租车恰好进入B加油站，求A加油站离甲地的距离.
高考英语听力测试期间，需要杜绝考点周围的噪音。如图，点A是某市一高考考点，在位于A考点南偏西15°方向距离125米的
点处有一消防队。在听力考试期间，消防队突然接到报警电话，告知在位于C点北偏东75°方向的F点处突发火灾，消防队必须立即赶往救火。已知消防车的警报声传播半径为100米，若消防车的警报声对听力测试造成影响，则消防车必须改道行驶。试问：消防车是否需要改道行驶？说明理由.（
取1.732）
青少年“心理健康”问题越来越引起社会的关注，某中学为了了解学校600名学生的心理健康状况，举行了一次“心理健康”知识测试，并随机抽取了部分学生的成绩（得分取正整数，满分为100分）作为样本，绘制了下面尚未完成的频率分布表和频率分布直方图.
| 分组 |
频数 |
频率 |
| 50.5～60.5 |
4 |
0.08 |
| 60.5～70.5 |
14 |
0.28 |
| 70.5～80.5 |
16 |
|
| 80.5～90. 5 |
||
| 90.5～100.5 |
10 |
0.20 |
| 合计 |
1.00 |
请解答下列问题：
（1）填写频率分布表中的空格，并补全频率分布直方图；
（2）若成绩在70分以上（不含70分）为心理健康状况良好，同时，若心理健康状况良好的人数占总人数的70％
以上，就表示该校学生的心理健康状况正常，否则就需要加强心理辅导。请根据上述数据分析该校学生是否需要加
强心理辅导，并说明理由.