滑板运动是极限运动的鼻祖,许多极限运动项目均由滑板项目延伸而来。如图所示是滑板运动的轨道,BC和DE是两段光滑圆弧形轨道,BC段的圆心为O点,圆心角为60º,半径OC与水平轨道CD垂直,水平轨道CD段粗糙且长8m。一运动员从轨道上的A点以3m/s的速度水平滑出,在B点刚好沿轨道的切线方向滑入圆弧轨道BC,经CD轨道后冲上DE轨道,到达E点时速度减为零,然后返回。已知运动员和滑板的总质量为60kg,B、E两点与水平面CD的竖直高度分别为h和H,且h=2m,H=2.8m,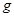 取10m/s2。求:
取10m/s2。求:

(1)运动员从A运动到达B点时的速度大小vB;
(2)轨道CD段的动摩擦因数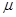 ;
;
(3)通过计算说明,第一次返回时,运动员能否回到B点?如能,请求出回到B点时速度的大小;如不能,则最后停在何处?
汽车前方120m处有一自行车正以6m/s的速度匀速前进,汽车以18m/s的速度追赶自行车,若两车在同一条公路不同车道上作同方向的直线运动,求:
(1)经多长时间,两车第一次相遇?
(2)若汽车追上自行车后立即刹车,汽车刹车过程中的加速度大小为2m/s2,则再经多长时间两车第二次相遇?
如图,在两水平极板间存在匀强电场和匀强磁场,电场方向竖直向下,磁场方向垂直于纸面向里。一带电粒子以某一速度沿水平直线通过两极板。若不计重力,下列四个物理量中哪一个改变时,粒子运动轨迹不会改变?()
| A.粒子速度的大小 |
| B.粒子所带电荷量 |
| C.电场强度 |
| D.磁感应强度 |
如图所示A、B为水平放置的足够长的平行板, 板间距离为d =1.0× m,A板中央有一电子源P,在纸面内能向各个方向发射速度在0~3.2×
m,A板中央有一电子源P,在纸面内能向各个方向发射速度在0~3.2×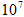 m/s范围内的电子,Q为P点正上方B板上的一点, 若垂直纸面加一匀强磁场, 磁感应强度B = 9.1×
m/s范围内的电子,Q为P点正上方B板上的一点, 若垂直纸面加一匀强磁场, 磁感应强度B = 9.1×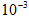 T,已知电子的质量m = 9.1×
T,已知电子的质量m = 9.1×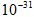 kg, 电子电量e = 1.6×
kg, 电子电量e = 1.6× C, 不计电子的重力和电子间相互作用力,且电子打到板上均被吸收, 并转移到大地. 求:
C, 不计电子的重力和电子间相互作用力,且电子打到板上均被吸收, 并转移到大地. 求:
(1)沿PQ方向射出的电子,击中A、B两板上的范围.
(2)若从P点发出的粒子能恰好击中Q点,则电子的发射方向(用图中θ角表示) 与电子速度的大小v之间应满足的关系及各自相应的取值范围.
如图所示,一轻绳一端连一小球B,另一端固定在O点,开始时球与O点在同一水平线上,轻绳拉直,在O点正下方距O点L处有一铁钉C,释放小球后,小球绕铁钉C恰好能做完整的竖直面内的圆周运动,重力加速度为g。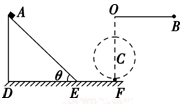
(1)求绳的长度.
(2)求小球第一次运动到最低点时的速度.
(3)若让小球自然悬挂,小球恰好与水平面接触于F点,小球质量为m,在水平面上固定有倾角为θ的斜面,斜面高为h,小球与斜面AE及水平面EF间的动摩擦因数均为μ,EF段长为s,让一质量与小球质量相等的滑块从斜面顶端由静止滑下,滑块与小球碰撞后粘在一起,结果两者一起恰好能绕C在竖直面内做圆周运动,则滑块与小球碰撞过程中损失的机械能是多少(不计滑块在E处碰撞的能量损失)?
用同种材料制成倾角37°的斜面和长水平面,斜面长15m且固定,一小物块从斜面顶端以沿斜面向下的初速度v0开始自由下滑,当v0=2m/s时,经过5s后小物块停在斜面上。多次改变v0的大小,记录下小物块从开始运动到最终停下的时间t,作出t-v0图象,如图所示,g="10" m/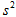 求:
求: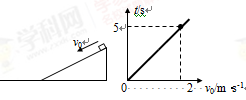
(1)小物块与该种材料间的动摩擦因数为多少?
(2)某同学认为,若小物块初速度为4m/s,则根据图象中t与v0成正比推导,可知小物块
运动时间为10s。以上说法是否正确?若不正确,说明理由并解出你认为正确的结果。