已知函数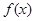 =
=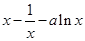 (
( ).
).
(1)若 在点
在点 处的切线与圆
处的切线与圆 相切,求
相切,求 的值;
的值;
(2)是否存在实数 ,使得
,使得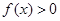 在
在 上恒成立?如果存在,试实数
上恒成立?如果存在,试实数 的取值范围;如果不存在,请说明理由.
的取值范围;如果不存在,请说明理由.
(本小题满分15分)已知椭圆 经过点
经过点 ,其离心率为
,其离心率为 .
.
(1) 求椭圆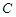 的方程;
的方程;
(2)设直线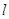 与椭圆
与椭圆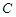 相交于
相交于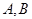 两点,以线段
两点,以线段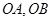 为邻边作平行四边形
为邻边作平行四边形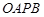 ,其中顶点
,其中顶点 在椭圆
在椭圆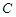 上,
上,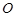 为坐标原点.求
为坐标原点.求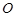 到直线
到直线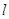 的距离的最小值.
的距离的最小值.
在等差数列 中,
中, ,其前
,其前 项和为
项和为 ,等比数列
,等比数列 的各项均为正数,
的各项均为正数, ,公比为
,公比为 ,且
,且 ,
,  .
.
(Ⅰ)求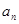 与
与 ;(Ⅱ)证明:
;(Ⅱ)证明: ≤
≤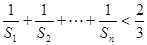 .
.
本题满分14分)已知向量 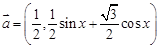 与
与 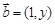 共线,设函数
共线,设函数 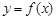 .
.
(I) 求函数 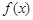 的周期及最大值;
的周期及最大值;
(II) 已知锐角 △ABC 中的三个内角分别为 A、B、C,若有  ,边 BC=
,边 BC=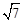 ,
,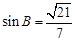 ,求 △ABC 的面积.
,求 △ABC 的面积.
在直角坐标系 中,以坐标原点
中,以坐标原点 为圆心的圆与直线:
为圆心的圆与直线: 相切.
相切.
(1)求圆 的方程;
的方程;
(2)若圆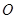 上有两点
上有两点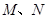 关于直线
关于直线 对称,且
对称,且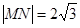 ,求直线MN的方程.
,求直线MN的方程.
已知函数 在
在 有最大值
有最大值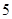 和最小值
和最小值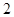 ,求
,求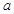 、
、 的值
的值