商场销售的某种促销商品每件售价为45元，成本为20元.对该商品进行促销：顾客每购买一件，可参加抽奖．抽奖箱中有大小完全相同的4个小球，编号分别为1,2,3,4．顾客从中任意取出1个球，记下上面的字后放回箱中，再从中任取1个球，重复以上操作，最多取4次，并规定若取出编号为4的小球，则停止取球．获奖规则如下：依次取到编号为1,2,3,4的小球为一等奖；不分顺序取到标有1,2,3,4的球，为二等奖；取到的4个球中有标有1,2,3的球为三等奖．
（1）求分别获得一、二、三等奖的概率；
（2）若奖励为返还现金，一等奖、二等奖、三等奖奖金数为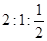
，统计表明：每天的销售y（件）与一等奖的奖金额x（元）的关系式为
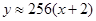，问x设定为多少最佳？并说明理由.
是定义在R上的奇函数，当
时，
，其中
且
.
的值；（2）求
（其中
），且
的图像在
轴右侧的第一个最高点的横坐标为
.
的值；（2）如果
在区间
上的最小值为
，求
的值.
.
的周期和单调递增区间；
的图象经过怎样变化得到.
的值．
，
,
，求
的值．
，
，
.
，
；
，求
的取值范围.