已知数列 满足
满足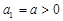 ,前n项和为Sn,Sn=
,前n项和为Sn,Sn=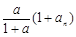 .
.
(1)求证: 是等比数列;
是等比数列;
(2)记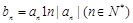 ,当
,当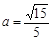 时是否存在正整数m,都有
时是否存在正整数m,都有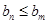 ?如果存在,求出m的值;如果不存在,请说明理由.
?如果存在,求出m的值;如果不存在,请说明理由.
在二项式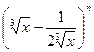 的展开式中,前三项系数的绝对值成等差数列.(1)求展开式的第四项;(2)求展开式的常数项;
的展开式中,前三项系数的绝对值成等差数列.(1)求展开式的第四项;(2)求展开式的常数项;
((本小题满分14分)
已知函数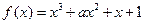 ,(
,(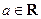 )
)
(Ⅰ)讨论函数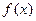 的单调区间;
的单调区间;
(Ⅱ)设函数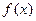 在区间
在区间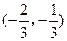 内是减函数,求
内是减函数,求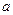 的取值范围.
的取值范围.
(本小题满分14分)
已知数列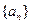 是正数组成的数列,其前n项和为
是正数组成的数列,其前n项和为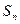 ,对于一切
,对于一切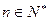 均有
均有 与2的等差中项等于
与2的等差中项等于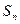 与2的等比中项.计算
与2的等比中项.计算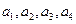 ;并由此猜想
;并由此猜想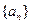 的通项公式
的通项公式 .
.
((本小题满分14分)
已知 ,复数
,复数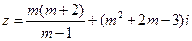 ,当
,当 为何值时,
为何值时,
(1) 为实数?
为实数?
(2) 为虚数?
为虚数?
(3) 为纯虚数?
为纯虚数?
((本小题满分14分)
某种产品的广告费支出x与销售额y(单位:百万元)之间有如下的对应数据:
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
50 |
60 |
70 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 =
= x+
x+ ;
;
(3)要使这种产品的销售额突破一亿元(含一亿元),则广告费支出至少为多少百万元?
(结果精确到0.1,参考数据:2×30+4×40+5×50+6×60+8×70=1390)。