如图所示折线段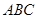 ,其中
,其中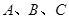 的坐标分别为
的坐标分别为 .
.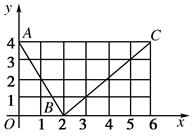
(1)若一抛物线 恰好过
恰好过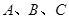 三点,求
三点,求 的解析式.
的解析式.
(2)函数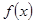 的图象刚好是折线段
的图象刚好是折线段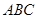 ,求
,求 的值和函数
的值和函数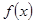 的解析式.
的解析式.
(本小题满分12分)如图已知平面 、
、 ,且
,且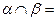 AB,PC⊥
AB,PC⊥ ,PD⊥
,PD⊥ ,C,D是垂足,试判断直线AB与CD的位置关系?并证明你的结论.
,C,D是垂足,试判断直线AB与CD的位置关系?并证明你的结论.

(本小题满分10分)选修4-5:不等式选讲
(Ⅰ)已知 都是正实数,求证:
都是正实数,求证: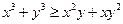 ;
;
(Ⅱ)已知 都是正实数,求证:
都是正实数,求证: .
.
(本小题满分10分)选修4-1:几何证明选讲
如图所示,AB是⊙O的直径,
G为AB延长线上的一点,GCD是⊙O的割线,过点<
G作AB的垂线,交AC的延长线于点E,交AD的延
长线于点F,过G作⊙O的切线,切点为H .
求证:(Ⅰ)C,D,F,E四点共圆;
(Ⅱ)GH2=GE·GF.
(本小题满分12分)设函数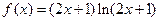 .
.
(Ⅰ)求函数f (x)在点(0, f (0))处的切线方程;
(Ⅱ)求f (x)的极小值;
(Ⅲ)若对所有的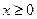 ,都有
,都有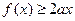 成立,求实数a的取值范围.
成立,求实数a的取值范围.
(本小题满分12分)一动圆与已知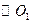 :
: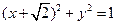 相外切,与
相外切,与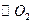 :
: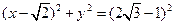 相内切.
相内切.
(Ⅰ)求动圆圆心的轨迹C;
(Ⅱ)若轨迹C与直线y="kx+m" (k≠0)相交于不同的两点M、N,当点A(0,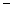 1)满足|
1)满足|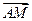 |=|
|=|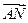 | 时,求m的取值范围.
| 时,求m的取值范围.