己知曲线 与x袖交于A,B两点,点P为x轴上方的一个动点,点P与A,B连线的斜率之积为-4
与x袖交于A,B两点,点P为x轴上方的一个动点,点P与A,B连线的斜率之积为-4
(1)求动点P的轨迹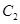 的方程;
的方程;
(2)过点B的直线 与
与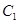 ,
,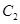 分别交于点M ,Q(均异于点A,B),若以MQ为直径的圆
分别交于点M ,Q(均异于点A,B),若以MQ为直径的圆
经过点A,求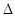 AMQ的面积.
AMQ的面积.
现有5名男生和3名女生.
(1)若3名女生必须相邻排在一起,则这8人站成一排,共有多少种不同的排法?
(2)若从中选5人,且要求女生只有2名, 站成一排,共有多少种不同的排法?
已知圆  关于直线
关于直线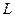 :
: 对称的圆为
对称的圆为 .
.
求圆 的方程
的方程
在圆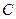 和圆
和圆  上各取点
上各取点 求线段
求线段 长的最小值.
长的最小值.
如图,在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形,现 有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是多少?
有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是多少?
某小组有男、女学生共13人,现从中选2人去完成一项任务。设每人当选的可能性相同。
⑴若选出的两人性别相同的概率为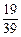 ,求选出的两人性别不同的概率;
,求选出的两人性别不同的概率;
⑵若已知该班男生有9人,求选出的两人性别不同的概率。
.已知两直线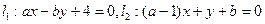 ,求满足下列条件的
,求满足下列条件的 、
、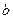 的值.直线
的值.直线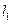 过点
过点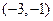 ,并且直线
,并且直线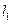 与直线
与直线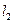 垂直;
垂直;