如图,在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形,现 有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是多少?
有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是多少?
已知数列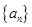 为等差数列,
为等差数列,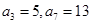 ,数列
,数列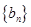 的前n项和为
的前n项和为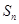 ,且有
,且有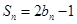 .
.
(Ⅰ)求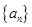 、
、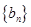 的通项公式;
的通项公式;
(Ⅱ)若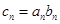 ,
,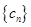 的前n项和为
的前n项和为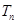 ,求
,求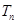 .
.
设命题 实数
实数 满足
满足 ,其中
,其中 ,命题
,命题 实数
实数 满足
满足 .
.
(Ⅰ)若 ,且
,且 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(Ⅱ)若 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.
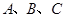 是我军三个炮兵阵地,
是我军三个炮兵阵地, 在
在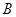 的正东方向相距6千米,
的正东方向相距6千米,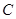 在
在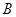 的北
的北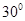 西方向,相距4千米,
西方向,相距4千米,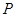 为敌炮阵地.某时刻,
为敌炮阵地.某时刻, 发现敌炮阵地的某信号,由于
发现敌炮阵地的某信号,由于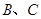 比
比 距
距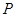 更远,因此4秒后,
更远,因此4秒后,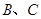 才同时发现这一信号(该信号的传播速度为每秒1千米).若从
才同时发现这一信号(该信号的传播速度为每秒1千米).若从 炮击敌阵地
炮击敌阵地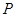 ,求炮击的方位角 .
,求炮击的方位角 .
在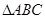 中满足条件
中满足条件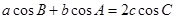 .
.
(Ⅰ)求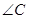 ;
;
(Ⅱ)若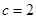 ,求三角形
,求三角形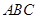 面积的最大值.
面积的最大值.
已知命题 方程
方程 的图象是焦点在
的图象是焦点在 轴上的双曲线;命题
轴上的双曲线;命题 方程
方程 无实根;又
无实根;又 为真,
为真, 为真,求实数
为真,求实数 的取值范围.
的取值范围.