在平面直角坐标系 中,已知点
中,已知点 ,
, ,
,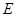 为动点,且直线
为动点,且直线 与直线
与直线 的斜率之积为
的斜率之积为 .
.
(1)求动点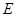 的轨迹
的轨迹 的方程;
的方程;
(2)设过点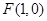 的直线
的直线 与曲线
与曲线 相交于不同的两点
相交于不同的两点 ,
, .若点
.若点 在
在 轴上,且
轴上,且 ,求点
,求点 的纵坐标的取值范围.
的纵坐标的取值范围.
从⊙O外一点P引圆的两条切线PA,PB及一条割线PCD,A,B为切点.
求证: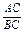 =
= .
.
已知:如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,DE⊥AC于E,DF⊥BC于F.求证:AE·BF·AB=CD3.
已知:如图所示,在△ABC中,D是BC的中点,F是BA延长线上的点,FD与AC交于点E.求证:AE·FB=EC·FA.
如图所示,已知D为△ABC的BC边
上一点,⊙O1经过点B,D,交AB于另一点E,⊙O2经过
点C,D,交AC于另一点F,⊙O1与⊙O2交于点G.
(1)求证:∠EAG=∠EFG;
(2)若⊙O2的半径为5,圆心O2到直线AC的距离为3,AC=10,AG切⊙O2于G,求线段AG的长.
如图所示,过圆
外一点
作它的一条切线,切点为
,过
点作直线
垂直于直线
,垂足为
. 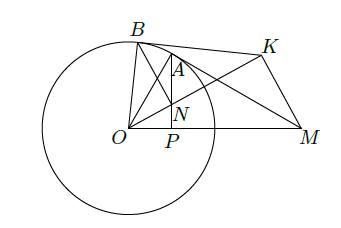
(1)证明:
;
(2)
为线段
上一点,直线
垂直于直线
,且交圆
于
点.过点
的切线交直线
于
.证明:
.