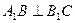(普通班)设函数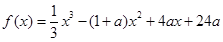 ,其中常数
,其中常数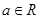 ;(1)讨论
;(1)讨论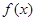 的单调性;(2)若
的单调性;(2)若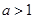 ,当
,当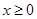 ,
,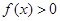 恒成立,求
恒成立,求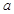 的取值范围。
的取值范围。
(实验班)已知椭圆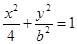 (0<b<2)的离心率等于
(0<b<2)的离心率等于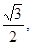 抛物线
抛物线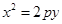 (p>0).
(p>0).
(1)若抛物线的焦点F在椭圆的顶点上,求椭圆和抛物线的方程;
(2)若抛物线的焦点F为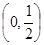 ,在抛物线上是否存在点P,使得过点P的切线与椭圆相交于A,B两点,且满足
,在抛物线上是否存在点P,使得过点P的切线与椭圆相交于A,B两点,且满足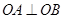 ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.
已知集合A={a1,a2,a3,a4},B={0,1,2,3},f是从A到B的映射.
(1)若B中每一元素都有原象,这样不同的f有多少个?
(2)若B中的元素0必无原象,这样的f有多少个?
(3)若f满足f(a1)+f(a2)+f(a3)+f(a4)=4,这样的f又有多少个?
12分)已知函数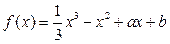 的图像在点
的图像在点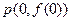 处的切线方程为
处的切线方程为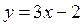 .
.
(Ⅰ)求实数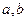 的值;
的值;
(Ⅱ)设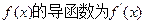 ,解不等式
,解不等式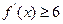 .
.
长方体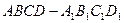 中,E是BC的中点,M、N分别是AE、
中,E是BC的中点,M、N分别是AE、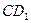 的中点,
的中点, . (1) 求证:
. (1) 求证: 平面
平面
(2)求异面直线AE与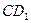 所成角的余弦值
所成角的余弦值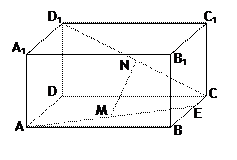
10分)某公司在过去几年内使用某种型号的灯管1000支,该公司对这些灯管的使用寿命
(单位:小时)进行了统计,统计结果如下表所示:
| 分组 |
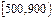 |
 |
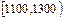 |
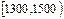 |
 |
 |
 |
| 组数 |
48 |
121 |
208 |
223 |
193 |
165 |
42 |
| 频率 |
(1)将各组的频率填入表中;
(2)根据上述统计结果,计算灯管使用寿命不足1500小时的频率;
(3)该公司某办公室新安装了这种型号的灯管3支,若将上述频率作为概率,试求至少有2支灯管的使用寿命不足1500小时的概率
如图所示的几何体中,已知平面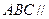 平面
平面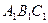 ,
, ,且
,且 ,
, ,
,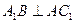 ,求证:
,求证: